
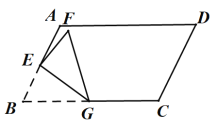
【题目】如图,![]() ,点G为边BC上一点,且
,点G为边BC上一点,且![]() ,点E为AB上一动点,将
,点E为AB上一动点,将![]() 沿
沿![]() 折叠,当点B的对应点F落在平行四边形的边上时,线段
折叠,当点B的对应点F落在平行四边形的边上时,线段![]() 的长为_______.
的长为_______.
【答案】![]()
【解析】
分两种情况:①当F在AB上时,由折叠的性质可知:∠BEG=90°;然后求得∠BGE=30°,最后根据30°所对的边是斜边的一半即可;②当F在AB上时,过A作AH⊥BG.先求出AG、BH的长,然后根据折叠的性质得到FG=BG=2![]() ,∠EFG=60°;再证明四边形AFGH是矩形,得到HG=BG-BH=2
,∠EFG=60°;再证明四边形AFGH是矩形,得到HG=BG-BH=2![]() -2;再根据等角对等边得到AE=AF=2
-2;再根据等角对等边得到AE=AF=2![]() -2,最后根据线段的和差解答即可.
-2,最后根据线段的和差解答即可.
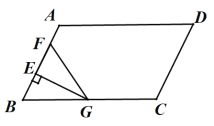
解:如图:当F在AB上时,由折叠的性质可知:∠BEG=90°
∵∠B=60°
∴∠BGE=30°
∵BG=2![]()
∴BE=![]() =
=![]() .
.
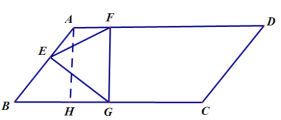
如图:当F在AB上时,过A作AH⊥BG,
∵∠B=60°,AB=4
∴AH=AB·sin∠B=4×![]() =2
=2![]() ,∠BAH=30°
,∠BAH=30°
∴BH=![]() =2
=2
由折叠的性质可得FG=BG=2![]() ,∠EFG=60°,
,∠EFG=60°,
∴AH//FG,即FG⊥AD,∠AFE=30°
∵平行四边形ABCD
∴AD∥BC
∴四边形AFGH是矩形, ∠BAF=180°-∠B=120°
∵HG=BG-BH=2![]() -2
-2
∴AF=HG=2![]() -2,∠AEF=180°-∠EAF-∠AFE=30°
-2,∠AEF=180°-∠EAF-∠AFE=30°
∴∠AEF=∠AFE
∴AE=AF=2![]() -2
-2
∴BE=AB-AE=4-(2![]() -2)=6-2
-2)=6-2![]() .
.
故答案为![]() 或6-2
或6-2![]() .
.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】为了提高学生身体素质,某市中小学开展阳光健步走活动,某数学兴趣小组收集了某校![]() 名学生一天行走的步数并记录如下:
名学生一天行走的步数并记录如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
对这![]() 个数据按组距
个数据按组距![]() 进行分组,并统计整理,绘制了如下尚不完整的统计图表.
进行分组,并统计整理,绘制了如下尚不完整的统计图表.
调查结果统计表:
组别 | 步数分组 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
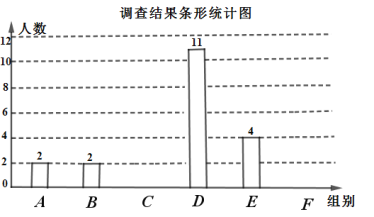
请根据以上信息,解答下列问题:
(1)填空:![]() ,
,![]()
(2)请补全条形统计图.
(3)这![]() 名学生一天行走步数的众数落在 组.
名学生一天行走步数的众数落在 组.
(4)根据科学研究,初中生一天的健步行走应不少于![]() 步,若该校有
步,若该校有![]() 名初中生,请你估计该校一天健步行走不少于
名初中生,请你估计该校一天健步行走不少于![]() 步的学生人数,并根据上述数据,给校方提出合理化的建议(有利于健步行走的)
步的学生人数,并根据上述数据,给校方提出合理化的建议(有利于健步行走的)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚去超市购买画笔,第一次花60元买了若干支A型画笔,第二次超市推荐了B型画笔,但B型画笔比A型画笔的单价贵2元,他又花100元买了相同支数的B型画笔.
(1)超市B型画笔单价多少元?
(2)小刚使用两种画笔后,决定以后使用B型画笔,但感觉其价格稍贵,和超市沟通后,超市给出以下优惠方案:一次购买不超过20支,则每支B型画笔打九折;若一次购买超过20支,则前20支打九折,超过的部分打八折.设小刚购买的B型画笔x支,购买费用为y元,请写出y关于x的函数关系式.
(3)在(2)的优惠方案下,若小刚计划用270元购买B型画笔,则能购买多少支B型画笔?
查看答案和解析>>
科目:初中数学 来源: 题型:
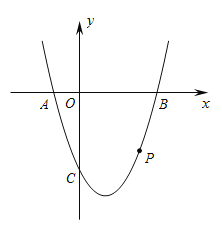
【题目】如图,抛物线![]() 与x轴相交于
与x轴相交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴相交于点
轴相交于点![]() .
.![]() 为抛物线上一点,横坐标为
为抛物线上一点,横坐标为![]() ,且
,且![]() .
.
⑴求此抛物线的解析式;
⑵当点![]() 位于
位于![]() 轴下方时,求
轴下方时,求![]() 面积的最大值;
面积的最大值;
⑶设此抛物线在点![]() 与点
与点![]() 之间部分(含点
之间部分(含点![]() 和点
和点![]() )最高点与最低点的纵坐标之差为
)最高点与最低点的纵坐标之差为![]() .
.
①求![]() 关于
关于![]() 的函数解析式,并写出自变量
的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
②当![]() 时,直接写出
时,直接写出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
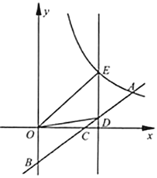
【题目】如图,在平面直角坐标系![]() 中,反比例函数
中,反比例函数![]() 的图像经过点
的图像经过点![]() ,点
,点![]() 在
在![]() 轴的负半轴上,
轴的负半轴上,![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 为线段
为线段![]() 的中点.
的中点.
(1)![]() ________,点
________,点![]() 的坐标为________;
的坐标为________;
(2)若点![]() 为线段
为线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴,交反比例函数图像于点
轴,交反比例函数图像于点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
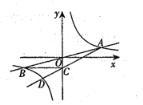
【题目】如图,在平面直角坐标系中,双曲线![]() 与直线
与直线![]() 相交于点
相交于点![]() 和B,过B点作
和B,过B点作![]() 轴于点C,连接AC,已知
轴于点C,连接AC,已知![]() .
.
(1)求![]() 的值;
的值;
(2)延长AC交双曲线于另一点D,求D的的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家商场平时以同样价格出售相同的商品,新冠疫情期间,为了减少库存,甲、乙两家商场打折促销,甲商场所有商品按9折出售,乙商场对一次购物中超过100元后的价格部分打8折.
⑴.以![]() (单位:元)表示商品原价,
(单位:元)表示商品原价,![]() (单位:元)表示实际购物金额,分别就两家商场的让利方式写出
(单位:元)表示实际购物金额,分别就两家商场的让利方式写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
⑵.新冠疫情期间如何选择这两家商场去购物更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
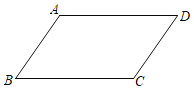
【题目】如图,在ABCD中,已知AD>AB.且AB=5.
(1)作∠BAD的平分线交BC于点E,在AD上截取AF=AB,连接EF;(保留作图痕迹,不写作法)
(2)若四边形ABEF的周长为a,求a的值
(3)根据(2),先化简W=(a+2)2﹣(a2+1),再求W的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与x轴交于点B(6,0),与y轴交于点A,与二次函数y=ax2的图象在第一象限内交于点C(3,3).

(1)求此一次函数与二次函数的表达式;
(2)若点D在线段AC上,与y轴平行的直线DE与二次函数图象相交于点E,∠ADO=∠OED,求点D坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com