
【题目】为了提高学生身体素质,某市中小学开展阳光健步走活动,某数学兴趣小组收集了某校![]() 名学生一天行走的步数并记录如下:
名学生一天行走的步数并记录如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
对这![]() 个数据按组距
个数据按组距![]() 进行分组,并统计整理,绘制了如下尚不完整的统计图表.
进行分组,并统计整理,绘制了如下尚不完整的统计图表.
调查结果统计表:
组别 | 步数分组 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
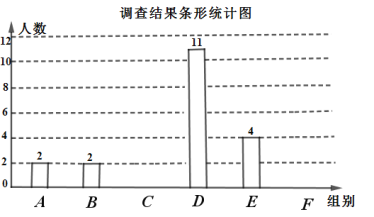
请根据以上信息,解答下列问题:
(1)填空:![]() ,
,![]()
(2)请补全条形统计图.
(3)这![]() 名学生一天行走步数的众数落在 组.
名学生一天行走步数的众数落在 组.
(4)根据科学研究,初中生一天的健步行走应不少于![]() 步,若该校有
步,若该校有![]() 名初中生,请你估计该校一天健步行走不少于
名初中生,请你估计该校一天健步行走不少于![]() 步的学生人数,并根据上述数据,给校方提出合理化的建议(有利于健步行走的)
步的学生人数,并根据上述数据,给校方提出合理化的建议(有利于健步行走的)
【答案】(1)3,8;(2)补全图形见解析;(3)D;(4)1800名;分析上述数据,可知该校还有五分之二的学生没有达标,所以要加强宣传,建议如下(合理即可)①加强宣传,舆论引导,让所有同学积极参与健步行走活动;②开展各种有意义的户外活动,让同学们动起来;③可以在课程结构上适当调整,增加户外活动课;④可以在上午及下午大课间组织学生到户外活动,如:上午大课间进行激情踏越式跑步,下午大课间进行广播体操比赛等
【解析】
(1)根据表格中的数据进一步分析即可得出相应的m、n的值;
(2)根据(1)中所求的数据补全条形统计图即可;
(3)根据众数的定义结合题意进一步分析即可;
(4)首先根据题意得出该30名学生中一天的健步行走不少于![]() 步所占的比例,由此进一步计算即可得出相应的结果,最后根据结果结合生活提出相应的建议即可.
步所占的比例,由此进一步计算即可得出相应的结果,最后根据结果结合生活提出相应的建议即可.
(1)根据表格数据可知:
当步数分组为![]() 时相关数据出现的频数为3,即
时相关数据出现的频数为3,即![]() ;
;
当步数分组为![]() 时相关数据出现的频数为8,即
时相关数据出现的频数为8,即![]() ;
;
故答案为:3,8;
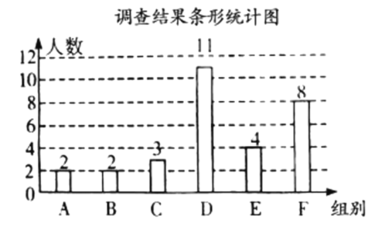
(2)补全的条形统计图如解图所示:
(3)∵![]() 组数据出现的频数最多,
组数据出现的频数最多,
∴学生一天行走步数的众数落在D组,
故答案为:D;
(4)![]() (名),
(名),
答:估计该校![]() 名初中生一天健步行走不少于
名初中生一天健步行走不少于![]() 步的人数为
步的人数为![]() 人,
人,
建议如下:
①加强宣传,舆论引导,让所有同学积极参与健步行走活动;
②开展各种有意义的户外活动,让同学们动起来;
③可以在课程结构上适当调整,增加户外活动课;
④可以在上午及下午大课间组织学生到户外活动,如:上午大课间进行激情踏越式跑步,下午大课间进行广播体操比赛等.


科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 轴于点
轴于点![]() ,且
,且![]() .
.
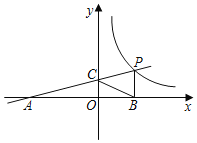
(1)求一次函数和反比例函数的解析式;
(2)点![]() 为反比例函数图象上使得四边形
为反比例函数图象上使得四边形![]() 为菱形的一点,点
为菱形的一点,点![]() 为
为![]() 轴上的一动点,当
轴上的一动点,当![]() 最大时,求点
最大时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如图.
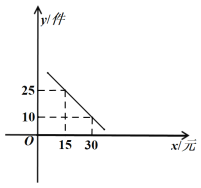
(1)求日销售量y(件)与每件产品的销售价x(元)之间的函数表达式;
(2)当每件产品的销售价定为多少元时,此时每日的销售利润最多,最多是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() ,抛物线
,抛物线![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
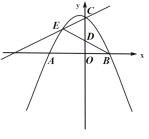

备用图
(1)求抛物线的解析式.
(2)点![]() 是直线
是直线![]() 上方的抛物线上一点,连接
上方的抛物线上一点,连接![]() 、
、![]() 、
、![]() ,
,![]() 与
与![]() 轴交于
轴交于![]() .
.
①点![]() 是
是![]() 轴上一动点,连接
轴上一动点,连接![]() ,当以
,当以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似时,求出线段
相似时,求出线段![]() 的长;
的长;
②点![]() 为
为![]() 轴左侧抛物线上一点,过点
轴左侧抛物线上一点,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,若
,若![]() ,请直接写出点
,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() ,
,![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,且与抛物线交于
,且与抛物线交于![]() 、
、![]() 两点.
两点.![]() 为抛物线上一动点(不与点
为抛物线上一动点(不与点![]() ,
,![]() 重合).
重合).
(1)求抛物线的解析式;
(2)当点![]() 在直线
在直线![]() 上方时,过点
上方时,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,
,![]() 轴交
轴交![]() 于点
于点![]() ,求
,求![]() 的最大值;
的最大值;
(3)设![]() 为直线
为直线![]() 上的点,以
上的点,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形能否构成平行四边形?若能,请直接写出点
为顶点的四边形能否构成平行四边形?若能,请直接写出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
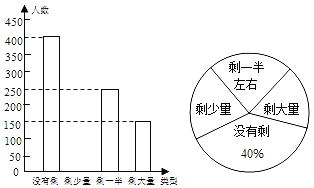
(1)这次被调查的同学共有 名,众数是 ;
(2)把条形统计图补充完整;
(3)通过数据分析,这次被调查的所有学生一餐浪费的食物大约可以供200人用一餐.据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学实践与综合课上,某兴趣小组同学用航拍无人机对某居民小区的1、2号楼进行测高实践,如图为实践时绘制的截面图.无人机从地面点B垂直起飞到达点A处,测得1号楼顶部E的俯角为67°,测得2号楼顶部F的俯角为40°,此时航拍无人机的高度为60米,已知1号楼的高度为20米,且EC和FD分别垂直地面于点C和D,点B为CD的中点,求2号楼的高度.(结果精确到0.1)(参考数据sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin67°≈0.92,cos67°≈0.39,tan67°≈2.36)
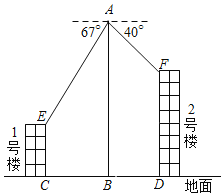
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com