
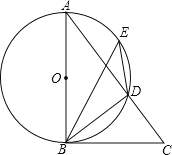
【题目】如图,AB是⊙O的直径,点E是![]() 上的一点,∠DBC=∠BED.
上的一点,∠DBC=∠BED.
(1)求证:BC是⊙O的切线;
(2)已知AD=3,CD=2,求BC的长.
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2 -(m+1)x+2(m-1)=0,
(1)求证:无论m取何值时,方程总有实数根;
(2)若等腰三角形腰长为4,另两边恰好是此方程的根,求此三角形的另外两条边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC 顶点 A(2,3).若以原点 O 为位似中心,画三角形 ABC
的位似图形△A′B′C′,使△ABC 与△A′B′C′的相似比为![]() ,则 A′的坐标为( )
,则 A′的坐标为( )
A. (3,![]() ) B. (
) B. (![]() ,6) C. (3,
,6) C. (3,![]() )或(-3,-
)或(-3,-![]() ) D. (
) D. (![]() ,6)或(-
,6)或(-![]() ,-6)
,-6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的农历三月初一为通州风筝节.这天,小刘同学正在江海明珠广场上放风筝,如图风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小宋同学,发现自己的位置与风筝和广场边旗杆PQ的顶点P在同一直线上.
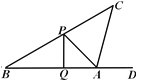
(1)已知旗杆高为10米,若在B处测得旗杆顶点P的仰角为30°,A处测得点P的仰角为45°,试求A、B之间的距离;
(2)此时,在A处背向旗杆又测得风筝的仰角为75°,若绳子在空中视为一条线段,求绳子AC为多少米?(结果可保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4.动点O在边CA上移动,且⊙O的半径为2.
(1)若圆心O与点C重合,则⊙O与直线AB________; (2)当OC等于________时,⊙O与直线AB相切.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣5,1),B(﹣2,2),C(﹣1,4),请按下列要求画图:
(1)将△ABC先向右平移4个单位长度、再向下平移1个单位长度,得到△A1B1C1,画出△A1B1C1;
(2)画出与△ABC关于原点O成中心对称的△A2B2C2,并直接写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把n个边长为1的正方形拼接成一排,求得tan∠BA1C=1,tan∠BA2C=![]() ,tan∠BA3C=
,tan∠BA3C=![]() ,计算tan∠BA4C=_____,…按此规律,写出tan∠BAnC=_____(用含n的代数式表示).
,计算tan∠BA4C=_____,…按此规律,写出tan∠BAnC=_____(用含n的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】凤城中学九年级(3)班的班主任让同学们为班会活动设计一个摸球方案,这些球除颜色外都相同,拟使中奖概率为50%.
(1)小明的设计方案:在一个不透明的盒子中,放入黄、白两种颜色的球共6个,搅匀后从中任意摸出1个球,摸到黄球则表示中奖,否则不中奖.如果小明的设计符合老师要求,则盒子中黄球应有 个,白球应有 个;
(2)小兵的设计方案:在一个不透明的盒子中,放入2个黄球和1个白球,搅匀后从中任意摸出2个球,摸到的2个球都是黄球则表示中奖,否则不中奖,该设计方案是否符合老师的要求?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某地区一条公路隧道入口在平面直角坐标系中的示意图,点A和A1、点B和B1分别关于y轴对称.隧道拱部分BCB1为一段抛物线,最高点C离路面AA1的距离为8 m,点B离路面AA1的距离为6 m,隧道宽AA1为16 m.
(1)求隧道拱部分BCB1对应的函数表达式.
(2)现有一大型货车,装载某大型设备后,宽为4 m,装载设备的顶部离路面均为7 m,问:它能否安全通过这个隧道?并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com