
【题目】如图,在ABCD中,已知AD>AB.且AB=5.
(1)作∠BAD的平分线交BC于点E,在AD上截取AF=AB,连接EF;(保留作图痕迹,不写作法)
(2)若四边形ABEF的周长为a,求a的值
(3)根据(2),先化简W=(a+2)2﹣(a2+1),再求W的值.
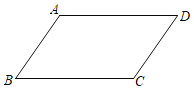
【答案】(1)见解析;(2)20;(3)83
【解析】
(1)利用尺规,根据要求作出图形即可.
(2)证明四边形ABEF是菱形即可解决问题.
(3)先利用乘法公式化简,再代入求值即可.
解:(1)如图,线段EF即为所求.
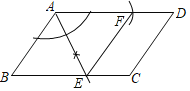
(2)∵AE平分∠BAD,
∴∠EAB=∠EAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAF=∠AEB,
∴∠BAE=∠BEA,
∴BA=BE,
∵AF=AB,
∴AF=BE,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴四边形ABEF是菱形,
∴四边形ABEF的周长为a=4AB=20.
(3)∵W=(a+2)2﹣(a2+1)=a2+4a+4﹣(a2+1)=4a+3,
∵a=20,
∴W=4×20+3=83.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
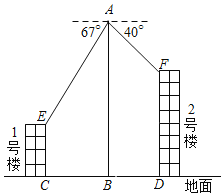
【题目】在数学实践与综合课上,某兴趣小组同学用航拍无人机对某居民小区的1、2号楼进行测高实践,如图为实践时绘制的截面图.无人机从地面点B垂直起飞到达点A处,测得1号楼顶部E的俯角为67°,测得2号楼顶部F的俯角为40°,此时航拍无人机的高度为60米,已知1号楼的高度为20米,且EC和FD分别垂直地面于点C和D,点B为CD的中点,求2号楼的高度.(结果精确到0.1)(参考数据sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin67°≈0.92,cos67°≈0.39,tan67°≈2.36)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
(1)求反比例函数的表达式;
(2)将直线l1:y=﹣![]() x向上平移后的直线l2与反比例函数y=
x向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
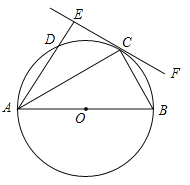
【题目】如图,AB为⊙O的直径,C、D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF⊥AD,交AD的延长线于点E,连接BC.
(1)求证:EF是⊙O的切线;
(2)若DE=1,BC=2,求劣弧![]() 的长l.
的长l.
查看答案和解析>>
科目:初中数学 来源: 题型:
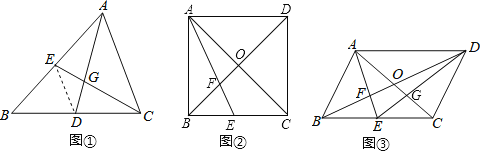
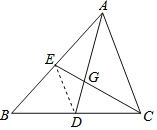
【题目】教材呈现:如图是华师版九年级上册数学教材第78页的部分内容.
例2 如图,在![]() 中,
中,![]() 分别是边
分别是边![]() 的中点,
的中点,![]() 相交于点
相交于点![]() ,求证:
,求证:![]() ,
,
证明:连结![]() .
.
请根据教材提示,结合图①,写出完整的证明过程.
结论应用:在![]() 中,对角线
中,对角线![]() 交于点
交于点![]() ,
,![]() 为边
为边![]() 的中点,
的中点,![]() 、
、![]() 交于点
交于点![]() .
.
(1)如图②,若![]() 为正方形,且
为正方形,且![]() ,则
,则![]() 的长为 .
的长为 .
(2)如图③,连结![]() 交
交![]() 于点
于点![]() ,若四边形
,若四边形![]() 的面积为
的面积为![]() ,则
,则![]() 的面积为 .
的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,2)与(0,3)之间(不包括这两点),对称轴为直线x=2.下列结论:abc<0;②9a+3b+c>0;③若点M(![]() ,y1),点N(
,y1),点N(![]() ,y2)是函数图象上的两点,则y1<y2;④﹣
,y2)是函数图象上的两点,则y1<y2;④﹣![]() <a<﹣
<a<﹣![]() .其中正确结论有( )
.其中正确结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,点
中,点![]() 分别是
分别是![]() 边上的两点,且
边上的两点,且![]() 分别交
分别交![]() 于
于![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() 平分
平分![]() ;③
;③![]() ;④
;④![]()
![]() .其中正确的结论是( )
.其中正确的结论是( )
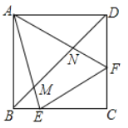
A.②③④B.①④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣2x+3经过点A(﹣3,0),P是抛物线上的一个动点.
(1)求该函数的表达式;
(2)如图所示,点P是抛物线上在第二象限内的一个动点,且点P的横坐标为t,连接AC,PA,PC.求△ACP的面积S关于t的函数关系式,并求出△ACP的面积最大时点P的坐标.
(3)连接BC,在抛物线上是否存在点P,使得∠PCA=∠OCB?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com