
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃНax2Љ2xЃЋ3ОЙ§ЕуA(Љ3ЃЌ0)ЃЌPЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЎ
ЃЈ1ЃЉЧѓИУКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉШчЭМЫљЪОЃЌЕуPЪЧХзЮяЯпЩЯдкЕкЖўЯѓЯоФкЕФвЛИіЖЏЕуЃЌЧвЕуPЕФКсзјБъЮЊtЃЌСЌНгACЃЌPAЃЌPCЃЎЧѓЁїACPЕФУцЛ§SЙигкtЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГіЁїACPЕФУцЛ§зюДѓЪБЕуPЕФзјБъЃЎ
ЃЈ3ЃЉСЌНгBCЃЌдкХзЮяЯпЩЯЪЧЗёДцдкЕуPЃЌЪЙЕУЁЯPCAЃНЁЯOCBЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉyЃНЃx2Ѓ2xЃЋ3ЃЛЃЈ2ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() Лђ(Ѓ4ЃЌЃ5)
Лђ(Ѓ4ЃЌЃ5)
ЁОНтЮіЁП
ЃЈ1ЃЉНЋЕуA(-3ЃЌ0)ДјШыНтЮіЪНЧѓНтМДПЩЃЛ
ЃЈ2ЃЉЙ§ЕуPзіДЙЯпЃЌдђ![]() ЃЌРћгУвбжЊAЁЂCЕузјБъПЩвдЧѓГіACжБЯпЕФНтЮіЪНЃЌДгЖјЕШЕНPЁЂQСНЕузјБъЃЌдйРћгУШ§НЧаЮУцЛ§ЙЋЪНЧѓНтМДПЩЃЛ
ЃЌРћгУвбжЊAЁЂCЕузјБъПЩвдЧѓГіACжБЯпЕФНтЮіЪНЃЌДгЖјЕШЕНPЁЂQСНЕузјБъЃЌдйРћгУШ§НЧаЮУцЛ§ЙЋЪНЧѓНтМДПЩЃЛ
ЃЈ3ЃЉзіГіИЈжњЯпЃЌНшжњШ§НЧКЏЪ§ЕУЕНЁЯPCAЃНЁЯOCBЕФЙиЯЕЃЌДгЖјЕУЕНБпгыБпЕФЙиЯЕЃЌЧѓНтГіЮДжЊЪ§ЃЎ
ЃЈ1ЃЉЖўДЮКЏЪ§![]() Й§ЕуA(-3ЃЌ0)ЃЌДњШыга0=9a+6+3ЃЌa=-1ЃЌ
Й§ЕуA(-3ЃЌ0)ЃЌДњШыга0=9a+6+3ЃЌa=-1ЃЌ
ЙЪЮЊДЫКЏЪ§НтЮіЪНЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЙ§ЕуPзїPN![]() AOгкЕуNЃЌНЛACгкЕуQЃЌ
AOгкЕуNЃЌНЛACгкЕуQЃЌ
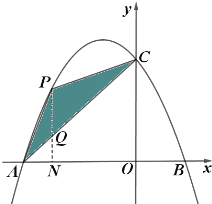
гЩЃЈ1ЃЉжЊЃЌC(0ЃЌ3)ЃЌЩшжБЯпACЕФНтЮіЪНЮЊy=kx+bЃЌЃЈk![]() 0ЃЉЃЌНЋA(-3ЃЌ0)ЁЂC(0ЃЌ3)ДњШыy=kx+bЃЌЕУ
0ЃЉЃЌНЋA(-3ЃЌ0)ЁЂC(0ЃЌ3)ДњШыy=kx+bЃЌЕУ![]() НтЕУ
НтЕУ![]() ЃЌ
ЃЌ
ЁржБЯпACЕФНтЮіЪНЮЊy=x+3ЃЌ
ЁпЕуPдкХзЮяЯп![]() ЩЯЃЌЕуQдкжБЯпACЩЯЃЌ
ЩЯЃЌЕуQдкжБЯпACЩЯЃЌ
ЁрP(tЃЌ![]() )ЃЌQ(tЃЌt+3)ЃЌ
)ЃЌQ(tЃЌt+3)ЃЌ
ЁрPQ=![]() =
=![]() ЃЌ
ЃЌ
![]() ЃЛ
ЃЛ
ЕБ![]() ЪБЃЌЁїACPЕФУцЛ§зюДѓЃЌ
ЪБЃЌЁїACPЕФУцЛ§зюДѓЃЌ![]() ЃЛ
ЃЛ
ЙЪSЙигкtЕФКЏЪ§ЙиЯЕЪН![]() ЃЌP
ЃЌP![]() ЃЛ
ЃЛ
ЃЈ3ЃЉХзЮяЯпЩЯДцдкЕуPЃЌЪЙЕУЁЯPCAЃНЁЯOCBЃЌ
Й§PЕузїPD![]() ACЃЌНЛACгкЕуDЃЌШчЭМ
ACЃЌНЛACгкЕуDЃЌШчЭМ
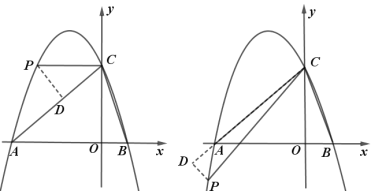
вбжЊХзЮяЯпЗНГЬЮЊ![]() ЃЌ
ЃЌ![]() ЃЌx=1ЃЌМДПЩЕУЕНB(1ЃЌ0)ЃЌ
ЃЌx=1ЃЌМДПЩЕУЕНB(1ЃЌ0)ЃЌ
дђгаOB=1ЃЌOC=3ЃЌ![]() ЃЌ
ЃЌ
ЕуPдкХзЮяЯпЩЯЃЌЩшЕуP(aЃЌ![]() )ЃЌжБЯпACЃКy=x+3ЃЌдђ
)ЃЌжБЯпACЃКy=x+3ЃЌдђ![]() ЃЌжБЯпPDЙ§ЕуPЃЌМДПЩЧѓГіPDЕФНтЮіЪНЮЊ
ЃЌжБЯпPDЙ§ЕуPЃЌМДПЩЧѓГіPDЕФНтЮіЪНЮЊ![]() ЃЌгжвђЮЊDЮЊPDгыACЕФНЛЕуЃЌСЊСЂЗНГЬзщга
ЃЌгжвђЮЊDЮЊPDгыACЕФНЛЕуЃЌСЊСЂЗНГЬзщга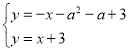 ЃЌНтЕУга
ЃЌНтЕУга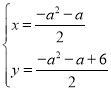 ЃЌМДD(
ЃЌМДD(![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
ЁпЁЯPCAЃНЁЯOCBЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр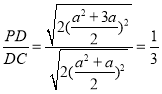 ЃЌНтЕУa=-4Лђa=
ЃЌНтЕУa=-4Лђa=![]() ЃЌ
ЃЌ
ЫљвдДцдкЕуP(-4ЃЌ-5)Лђ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
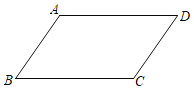
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌвбжЊADЃОABЃЎЧвABЃН5ЃЎ
ЃЈ1ЃЉзїЁЯBADЕФЦНЗжЯпНЛBCгкЕуEЃЌдкADЩЯНиШЁAFЃНABЃЌСЌНгEFЃЛЃЈБЃСєзїЭМКлМЃЃЌВЛаДзїЗЈЃЉ
ЃЈ2ЃЉШєЫФБпаЮABEFЕФжмГЄЮЊaЃЌЧѓaЕФжЕ
ЃЈ3ЃЉИљОнЃЈ2ЃЉЃЌЯШЛЏМђWЃНЃЈa+2ЃЉ2ЉЃЈa2+1ЃЉЃЌдйЧѓWЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y=kx+bЕФЭМЯѓгыxжсНЛгкЕуBЃЈ6,0ЃЉЃЌгыyжсНЛгкЕуAЃЌгыЖўДЮКЏЪ§y=ax2ЕФЭМЯѓдкЕквЛЯѓЯоФкНЛгкЕуCЃЈ3,3ЃЉЃЎ

(1)ЧѓДЫвЛДЮКЏЪ§гыЖўДЮКЏЪ§ЕФБэДяЪНЃЛ
(2)ШєЕуDдкЯпЖЮACЩЯЃЌгыyжсЦНааЕФжБЯпDEгыЖўДЮКЏЪ§ЭМЯѓЯрНЛгкЕуEЃЌЁЯADO=ЁЯOEDЃЌЧѓЕуDзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() жаЃЌ
жаЃЌ![]() ЃЌDЁЂEЗжБ№ЪЧБп
ЃЌDЁЂEЗжБ№ЪЧБп![]() ЁЂ
ЁЂ![]() ЕФжаЕуЃЎНЋ
ЕФжаЕуЃЎНЋ![]() ШЦЕуEа§зЊ180ЖШЃЌЕУ
ШЦЕуEа§зЊ180ЖШЃЌЕУ![]() ЃЎ
ЃЎ
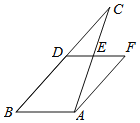
ЃЈ1ЃЉХаЖЯЫФБпаЮ![]() ЕФаЮзДЃЌВЂжЄУїЃЛ
ЕФаЮзДЃЌВЂжЄУїЃЛ
ЃЈ2ЃЉвбжЊ![]() ЃЌ
ЃЌ![]() ЃЌЧѓЫФБпаЮ
ЃЌЧѓЫФБпаЮ![]() ЕФУцЛ§SЃЎ
ЕФУцЛ§SЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
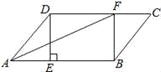
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌЙ§ЕуDзїDEЁЭABгкЕуEЃЌЕуFдкБпCDЩЯЃЌCF=AEЃЌСЌНгAFЃЌBF.
(1)ЧѓжЄЃКЫФБпаЮBFDEЪЧОиаЮЃЛ
(2)вбжЊЁЯDAB=60ЁуЃЌAFЪЧЁЯDABЕФЦНЗжЯпЃЌШєAD=3ЃЌЧѓDCЕФГЄЖШ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
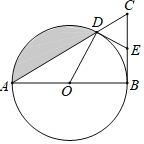
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯABCЃН90ЁуЃЌвдABЮЊжБОЖЕФЁбOНЛACгкЕуDЃЌЕуEЮЊBCЕФжаЕуЃЌСЌНгODЁЂDEЃЎ
ЃЈ1ЃЉЧѓжЄЃКDEЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєЁЯBACЃН30ЁуЃЌABЃН12ЃЌЧѓвѕгАВПЗжЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
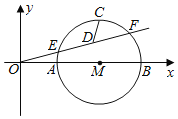
ЁОЬтФПЁПШчЭМЃЌAЃЈ2ЃЌ0ЃЉЁЂBЃЈ6ЃЌ0ЃЉЃЌвдABЮЊжБОЖзїЁбMЃЌЩфЯпOFНЛЁбMгкEЁЂFСНЕуЃЌCЮЊЛЁABЕФжаЕуЃЌDЮЊEFЕФжаЕуЃЎЕБЩфЯпOFШЦOЕуа§зЊЪБЃЌCDЕФзюаЁжЕЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌEЪЧBCЕФжаЕуЃЌЧвЁЯAECЃНЁЯDCEЃЌдђЯТСаНсТлВЛе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
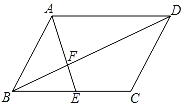
A.SЁїAFDЃН2SЁїEFBB.BFЃН![]() DF
DF
C.AEЃНDCD.ЁЯAEBЃНЁЯADC
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
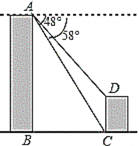
ЁОЬтФПЁПШчЭМЃЌМзЁЂввСНзљНЈжўЮяЕФЫЎЦНОрРы![]() ЮЊ
ЮЊ![]() ЃЌДгМзЕФЖЅВП
ЃЌДгМзЕФЖЅВП![]() ДІВтЕУввЕФЖЅВП
ДІВтЕУввЕФЖЅВП![]() ДІЕФИЉНЧЮЊ48ЁуЃЌВтЕУЕзВП
ДІЕФИЉНЧЮЊ48ЁуЃЌВтЕУЕзВП![]() ДІЕФИЉНЧЮЊ53ЁуЃЌЧѓМзЁЂввНЈжўЮяЕФИпЖШ
ДІЕФИЉНЧЮЊ53ЁуЃЌЧѓМзЁЂввНЈжўЮяЕФИпЖШ![]() КЭ
КЭ![]() ЃЈНсЙћгУКЌЗЧЬижщНЧЕФШ§НЧКЏЪ§БэЪОМДПЩЃЉЃЎ
ЃЈНсЙћгУКЌЗЧЬижщНЧЕФШ§НЧКЏЪ§БэЪОМДПЩЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com