
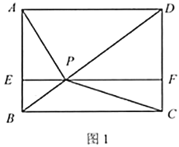
【题目】(1)如图1,点![]() 为矩形
为矩形![]() 对角线
对角线![]() 上一点,过点
上一点,过点![]() 作
作![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .若
.若![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() ________;
________;
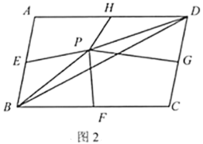
(2)如图2,点![]() 为
为![]() 内一点(点
内一点(点![]() 不在
不在![]() 上),点
上),点![]() 、
、![]() 、
、![]() 、
、![]() 分别为各边的中点.设四边形
分别为各边的中点.设四边形![]() 的面积为
的面积为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() (其中
(其中![]() ),求
),求![]() 的面积(用含
的面积(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
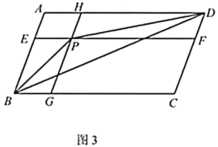
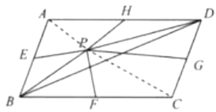
(3)如图3,点![]() 为
为![]() 内一点(点
内一点(点![]() 不在
不在![]() 上)过点
上)过点![]() 作
作![]() ,
,![]() ,与各边分别相交于点
,与各边分别相交于点![]() 、
、![]() 、
、![]() 、
、![]() .设四边形
.设四边形![]() 的面积为
的面积为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() (其中
(其中![]() ),求
),求![]() 的面积(用含
的面积(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
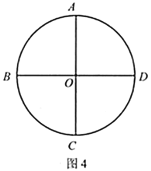
(4)如图4,点![]() 、
、![]() 、
、![]() 、
、![]() 把
把![]() 四等分.请你在圆内选一点
四等分.请你在圆内选一点![]() (点
(点![]() 不在
不在![]() 、
、![]() 上),设
上),设![]() 、
、![]() 、
、![]() 围成的封闭图形的面积为
围成的封闭图形的面积为![]() ,
,![]() 、
、![]() 、
、![]() 围成的封闭图形的面积为
围成的封闭图形的面积为![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() .根据你选的点
.根据你选的点![]() 的位置,直接写出一个含有
的位置,直接写出一个含有![]() 、
、![]() 、
、![]() 、
、![]() 的等式(写出一种情况即可).
的等式(写出一种情况即可).
【答案】(1)12;(2)![]() ;(3)
;(3)![]() ;(4)答案不唯一
;(4)答案不唯一
【解析】
(1)过P点作AB的平行线MN,根据S矩形AEPM+S矩形DFPM=S矩形CFPN+S矩形DFPM=S矩形ABCD-S矩形BEPN从而得到,S矩形AEPM =S矩形CFPN进而得到![]() 与
与![]() 的关系,从而求出结果.
的关系,从而求出结果.
(2)连接![]() 、
、![]() ,设
,设![]() ,
,![]() ,根据图形得到
,根据图形得到![]() ,求出
,求出![]() ,
, ![]() ,最终求出结果.
,最终求出结果.
(3)易知![]() ,
,![]() ,导出
,导出![]() ,再由
,再由![]() 的关系,即可可求解.
的关系,即可可求解.
(4)连接ABCD的得到正方形,根据(3)的方法,进行分割可找到面积之间的关系.
(1)过P点作AB∥MN,
∵S矩形AEPM+S矩形DFPM=S矩形CFPN+S矩形DFPM=S矩形ABCD-S矩形BEPN,
又∵![]()
∴![]()
∴![]()
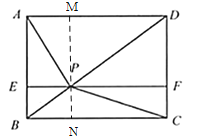
(2)如图,连接![]() 、
、![]() ,
,
在![]() 中,因为点E是
中,因为点E是![]() 中点,
中点,
可设![]() ,
,
同理,![]() ,
,
所以![]() ,
,
![]() .
.
所以![]() ,
,
所以![]() ,所以
,所以![]() .
.
![]() .
.
(3)易证四边形![]() 、四边形
、四边形![]() 是平行四边形.
是平行四边形.
所以![]() ,
,![]() .
.
所以![]() ,
,
![]() .
.
(4)
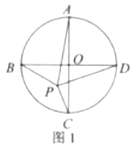
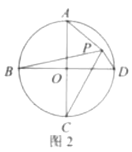
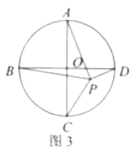
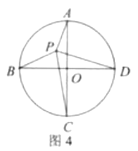
答案不唯一,如:
如图1或图2,此时![]() ;
;
如图3或图4,此时![]() .
.


科目:初中数学 来源: 题型:
【题目】如图, 在平面直角坐标系中, ![]() 的顶点
的顶点![]() 与原点重合,点
与原点重合,点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() 按以下步骤作图:①以点
按以下步骤作图:①以点![]() 为圆心,适当长度为半径作
为圆心,适当长度为半径作![]() 弧,分别交边
弧,分别交边![]() ,
,![]() 于点
于点![]() ,
,![]() ;②分别以点
;②分别以点![]() ,
,![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧, 两弧在
的长为半径作弧, 两弧在![]() 内交于点
内交于点![]() ;③作射线
;③作射线![]() ,交边
,交边![]() 于点
于点![]() .若
.若![]() ,
,![]() ,则点
,则点![]() 的坐标为( )
的坐标为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校“校园主持人大赛”结束后,将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图.部分信息如下:
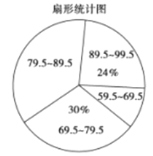
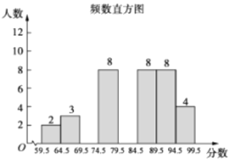
(1)本次比赛参赛选手共有________人,扇形统计图中“79.5~89.5”这一范围的人数占总参赛人数的百分比为________;
(2)补全图2频数直方图;
(3)赛前规定,成绩由高到低前40%的参赛选手获奖.某参赛选手的比赛成绩为88分,试判断他能否获奖,并说明理由;
(4)成绩前四名是2名男生和2名女生,若他们中任选2人作为该校文艺晚会的主持人,试求恰好选中1男1女为主持人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,P是对角线BD上的一点,过点C作CQ∥DB,且CQ=DP,连接AP、BQ、PQ.
(1)求证:△APD≌△BQC;
(2)若∠ABP+∠BQC=180°,求证:四边形ABQP为菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2021年起,江苏省高考采用“![]() ”模式:“3”是指语文、数学、外语3科为必选科目,“1”是指在物理、历史2科中任选科,“2”是指在化学、生物、思想政治、地理4科中任选2科.
”模式:“3”是指语文、数学、外语3科为必选科目,“1”是指在物理、历史2科中任选科,“2”是指在化学、生物、思想政治、地理4科中任选2科.
(1)若小丽在“1”中选择了历史,在“2”中已选择了地理,则她选择生物的概率是________;
(2)若小明在“1”中选择了物理,用画树状图的方法求他在“2中选化学、生物的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某小型汽车的侧面示意图,其中矩形ABCD表示该车的后备箱,在打开后备箱的过程中,箱盖ADE可以绕点A逆时针方向旋转,当旋转角是50度时,箱盖落在![]() 的位置(如图2),已知
的位置(如图2),已知![]()
![]()
![]()
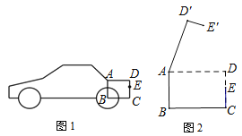
(1)求点![]() 到
到![]() 的距离;(结果保留整数)
的距离;(结果保留整数)
(2)求![]() 两点之间的距离.(结果保留整数)
两点之间的距离.(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与双曲线
,与双曲线![]() 在第三象限交于
在第三象限交于![]() 两点,且
两点,且 ![]() ;下列等边三角形
;下列等边三角形![]() ,
,![]() ,
,![]() ,……的边
,……的边![]() ,
,![]() ,
,![]() ,……在
,……在![]() 轴上,顶点
轴上,顶点![]() ……在该双曲线第一象限的分支上,则
……在该双曲线第一象限的分支上,则![]() = ____,前25个等边三角形的周长之和为 _______.
= ____,前25个等边三角形的周长之和为 _______.
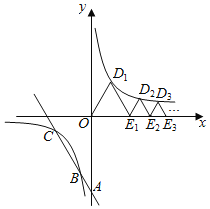
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“微信运动”被越来越多的人关注和喜爱,某数学兴趣小组随机调查了我区50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
0≤x<4000 | 8 | 0.16 |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | a |
12000≤x<16000 | b | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | 2 | 0.04 |
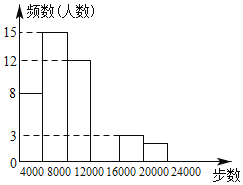
请根据以上信息,解答下列问题:
(1)写出a,b的值并补全频数分布直方图;
(2)我市约有5000名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步)的两名教师与大家分享心得,用树形图或列表法求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙A过OBCD的三顶点O、D、C,边OB与⊙A相切于点O,边BC与⊙O相交于点H,射线OA交边CD于点E,交⊙A于点F,点P在射线OA上,且∠PCD=2∠DOF,以O为原点,OP所在的直线为x轴建立平面直角坐标系,点B的坐标为(0,﹣2).
(1)若∠BOH=30°,求点H的坐标;
(2)求证:直线PC是⊙A的切线;
(3)若OD=![]() ,求⊙A的半径.
,求⊙A的半径.
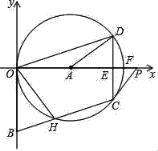
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com