
【题目】如图:点E、F为线段BD的两个三等分点,四边形AECF是菱形,且菱形AECF的周长为20,BD为24,则四边形ABCD的面积为( )
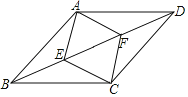
A.24B.36C.72D.144
【答案】C
【解析】
根据菱形的对角线互相垂直平分可得AC⊥BD,AO=OC,EO=OF,再求出BO=OD,证明四边形ABCD是菱形,根据菱形的四条边都相等求出边长AE,根据菱形的对角线互相平分求出OE,然后利用勾股定理列式求出AO,再求出AC,最后根据四边形的面积等于对角线乘积的一半列式计算即可得解.
解:如图,连接AC交BD于点O,
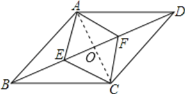
∵四边形AECF是菱形,
∴AC⊥BD,AO=OC,EO=OF,
又∵点E、F为线段BD的两个三等分点,
∴BE=FD,
∴BO=OD,
∵AO=OC,
∴四边形ABCD为平行四边形,
∵AC⊥BD,
∴四边形ABCD为菱形;
∵四边形AECF为菱形,且周长为20,
∴AE=5,
∵BD=24,点E、F为线段BD的两个三等分点,
∴EF=8,OE=![]() EF=
EF=![]() ×8=4,
×8=4,
由勾股定理得,AO=![]() =
=![]() =3,
=3,
∴AC=2AO=2×3=6,
∴S四边形ABCD=![]() BDAC=
BDAC=![]() ×24×6=72;
×24×6=72;
故选:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.
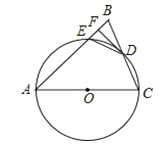
(1)求证:直线DF与⊙O相切;
(2)若AE=7,BC=6,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,与y轴交于C点,M点在抛物线的对称轴上,当点M到点B的距离与到点C的距离之和最小时,点M的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爸爸想送小明一个书包和一辆自行车作为新年礼物,在甲、乙两商场都发现同款的自行车单价相同,书包单价也相同,自行车和书包单价之和为452元,且自行车的单价比书包的单价4倍少8元.
(1)求自行车和书包单价各为多少元;
(2)新年来临赶上商家促销,乙商场所有商品打八五折(即8.5折)销售,甲全场购物毎满100元返购物券30元(即不足100元不返券,满100元送30元购物券,满200元送60元购物券),并可当场用于购物,购物券全场通用.但爸爸只带了400元钱,如果他只在同一家商场购买看中的两样物品,在哪一家买更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【新知理解】
如图①,若点![]() 、
、![]() 在直线l同侧,在直线l上找一点
在直线l同侧,在直线l上找一点![]() ,使
,使![]() 的值最小.
的值最小.
作法:作点![]() 关于直线l的对称点
关于直线l的对称点![]() ,连接
,连接![]() 交直线l于点
交直线l于点![]() ,则点
,则点![]() 即为所求.
即为所求.
【解决问题】
如图②,![]() 是边长为6cm的等边三角形
是边长为6cm的等边三角形![]() 的中线,点
的中线,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,则
上,则![]() 的最小值为 cm;
的最小值为 cm;
【拓展研究】
如图③,在四边形![]() 的对角线
的对角线![]() 上找一点
上找一点![]() ,使
,使![]() .(保留作图痕迹,并对作图方法进行说明)
.(保留作图痕迹,并对作图方法进行说明)
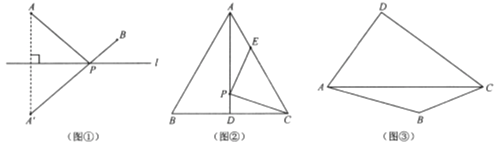
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中央电视台的“朗读者”节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本数最少的有5本,最多的有8本,并根据调查结果绘制了不完整的图表:
本数(本) | 人数(人数) | 百分比 |
5 | a | 0.2 |
6 | 18 | 0.36 |
7 | 14 | b |
8 | 8 | 0.16 |
合计 | c | 1 |
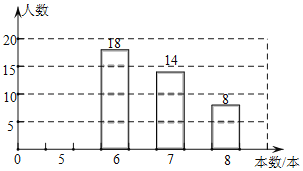
根据以上提供的信息,解答下列问题:
(1)a=_____,b=_____,c=______;
(2)补全上面的条形统计图;
(3)若该校八年级共有1200名学生,请你分析该校八年级学生课外阅读7本及以上的有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】情境![]() :小芳离开家去学校上学,走了一段路后,发现自己作业本忘家里了,于是返回家里找到作业本,然后又赶快去学校;
:小芳离开家去学校上学,走了一段路后,发现自己作业本忘家里了,于是返回家里找到作业本,然后又赶快去学校;
情境![]() :小明从家出发去图书馆还书,走了一段路程后,发现时间有点紧张,便以更快的速度前进.
:小明从家出发去图书馆还书,走了一段路程后,发现时间有点紧张,便以更快的速度前进.

(1)情境![]() 所对应的函数图象分别是_______,_______(填写序号);
所对应的函数图象分别是_______,_______(填写序号);
(2)请你为剩下的函数图象写出一个适合的情景.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列问题:
(1)阅读理解:
如图1,在![]() 中,若
中,若![]() ,
,![]() ,求
,求![]() 边上的中线
边上的中线![]() 的取值范围.
的取值范围.
解决此问题可以用如下方法:延长![]() 到点
到点![]() 使
使![]() ,再连接
,再连接![]() (或将
(或将![]() 绕着
绕着![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,把
,把![]() 、
、![]() ,
,![]() 集中在
集中在![]() 中,利用三角形三边的关系即可判断.中线
中,利用三角形三边的关系即可判断.中线![]() 的取值范围是______.
的取值范围是______.
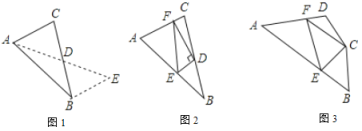
(2)问题解决:
如图2,在![]() 中,
中,![]() 是
是![]() 边上的中点,
边上的中点,![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() .
.
(3)问题拓展:
如图3,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,以
,以![]() 为顶点作一个
为顶点作一个![]() 角,角的两边分别交
角,角的两边分别交![]() ,
,![]() 于
于![]() 、
、![]() 两点,连接
两点,连接![]() ,探索线段
,探索线段![]() ,
,![]() ,
,![]() 之间的数量关系,并加以证明.
之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,要使△ABC和△QPA全等,则AP= ______ .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com