
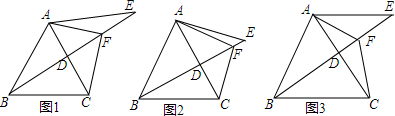
分析 (1)证△EAF≌△CAF,推出EF=CF,∠E=∠ACF,根据等腰三角形性质推出∠E=∠ABF,即可得出答案;
(2)在FB上截取BM=CF,连接AM,证△ABM≌△ACF,推出EF=FC=BM,AF=AM,推出△AMF是等边三角形,推出MF=AF,即可得出答案;
(3)连接CF,延长BA、CF交N,证△BFC≌△BFN,推出CN=2CF=2EF,证△BAD≌△CAN,推出BD=CN,即可得出答案.
解答 证明:(1)∠CFB=∠CAB,
∵AF平分∠CAE,
∴∠EAF=∠CAF,
∵AB=AC,AB=AE,
∴AE=AC,
在△ACF和△AEF中,
$\left\{\begin{array}{l}{AE=AC}\\{∠EAF=∠CAF}\\{AF=AF}\end{array}\right.$,
∴△ACF≌△AEF(SAS),
∴∠E=∠ACF,
∵AB=AE,
∴∠E=∠ABE,
∴∠ABE=∠ACF,
∵∠ADB=∠CDF,
∴∠CFB=∠CAB;
(2)如图2,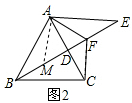 ∵△ACF≌△AEF,
∵△ACF≌△AEF,
∴EF=CF,∠E=∠ACF=∠ABM,
在FB上截取BM=CF,连接AM,
在△ABM和△ACF中,
$\left\{\begin{array}{l}{AB=AC}\\{∠ABM=∠ACF}\\{BM=CF}\end{array}\right.$,
∴△ABM≌△ACF(SAS),
∴AM=AF,∠BAM=∠CAF,
∵AB=AC,∠ABC=60°,
∴△ABC是等边三角形,
∴∠BAC=60°,
∴∠MAF=∠MAC+∠CAF=∠MAC+∠BAM=∠BAC=60°,
∵AM=AF,
∴△AMF为等边三角形,
∴AF=AM=MF,
∴AF+EF=BM+MF=FB,
∵AF=m,EF=n,
即FB=m+n;
(3)如图3,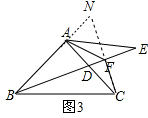 延长BA、CF交于N,
延长BA、CF交于N,
∵AE∥BC,
∴∠E=∠EBC,
∵AB=AE,
∴∠ABE=∠E,
∴∠ABF=∠CBF,
∵∠ABC=45°,
∴∠ABF=∠CBF=22.5°,∠ACB=45°,∠BAC=180°-45°-45°=90°,
∴∠ACF=∠ABF=22.5°,
∴∠BFC=180°-22.5°-45°-22.5°=90°,
∴∠BFN=∠BFC=90°,
在△BFN和△BFC中
$\left\{\begin{array}{l}{∠NBF=∠CBF}\\{BF=BF}\\{∠BFN=∠BFC}\end{array}\right.$
∴△BFN≌△BFC(ASA),
∴CF=FN,
即CN=2CF=2EF,
∵∠BAC=90°,
∴∠NAC=∠BAD=90°,
在△BAD和△CAN中
$\left\{\begin{array}{l}{∠ABD=∠ACN}\\{AB=AC}\\{∠BAD=∠CAN}\end{array}\right.$
∴△BAD≌△CAN(ASA),
由第二问得CF=EF,
∴BD=CN=2CF=2EF.
点评 本题考查了等边三角形的性质和判定,全等三角形的性质和判定,等腰三角形的性质和判定的应用,主要考查学生综合运用性质进行推理的能力,难度偏大.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | -5 | B. | 5 | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
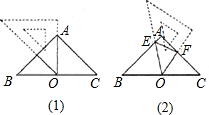 在△ABC中,AB=AC=2,∠BAC=90°,取一块含45°角的直角三角形纸板,将45°角的顶点放在斜边BC的中点O处(如图①),顺时针方向旋转三角尺,使45°角的两边与AB、AC分别交于点E、F(如图②).设BE=x,CF=y,求y与x的函数表达式,并写出x的取值范围.
在△ABC中,AB=AC=2,∠BAC=90°,取一块含45°角的直角三角形纸板,将45°角的顶点放在斜边BC的中点O处(如图①),顺时针方向旋转三角尺,使45°角的两边与AB、AC分别交于点E、F(如图②).设BE=x,CF=y,求y与x的函数表达式,并写出x的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k≤2 | B. | k≤2且k≠1 | C. | k<2且k≠1 | D. | k≥2 |
查看答案和解析>>
科目:初中数学 来源:2017届四川省遂宁市九年级上学期期末考试数学试卷(解析版) 题型:解答题
一个不透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另外有一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图所示).
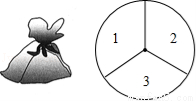
(1)从口袋中摸出一个小球,所摸球上的数字大于2的概率为 ;
(2)小龙和小东想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于5,那么小龙去;否则小东去.你认为游戏公平吗?请用树状图或列表法说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com