
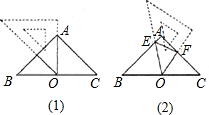
 在△ABC中,AB=AC=2,∠BAC=90°,取一块含45°角的直角三角形纸板,将45°角的顶点放在斜边BC的中点O处(如图①),顺时针方向旋转三角尺,使45°角的两边与AB、AC分别交于点E、F(如图②).设BE=x,CF=y,求y与x的函数表达式,并写出x的取值范围.
在△ABC中,AB=AC=2,∠BAC=90°,取一块含45°角的直角三角形纸板,将45°角的顶点放在斜边BC的中点O处(如图①),顺时针方向旋转三角尺,使45°角的两边与AB、AC分别交于点E、F(如图②).设BE=x,CF=y,求y与x的函数表达式,并写出x的取值范围. 分析 根据等腰直角三角形的性质得到BC=2$\sqrt{2}$,∠B=∠C=45°,由点O是BC 的中点,得到BO=CO=$\sqrt{2}$根据三角形的内角和和平角的定义得到∠BEO=∠COF,证得△BOE∽△COF,根据相似三角形的性质即可得到结论.
解答 解:∵AB=AC=2,∠BAC=90°,
∴BC=2$\sqrt{2}$,∠B=∠C=45°,
∵点O是BC 的中点,
∴BO=CO=$\sqrt{2}$,∵∠EOF=45°,
∴∠BEO+∠BOE=135°,∠BOE+∠COF=135°,
∴∠BEO=∠COF,
∴△BOE∽△COF,
∴$\frac{BE}{OC}=\frac{BO}{CF}$,
即$\frac{x}{\sqrt{2}}=\frac{\sqrt{2}}{y}$,
∴xy=2,
∴y与x的函数表达式:y=$\frac{2}{x}$ (0<x≤2).
点评 本题考查了相似三角形的判定和性质,等腰直角三角形的性质,熟练掌握相似三角形的判定和性质是解题的关键.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:选择题
| A. | 4组 | B. | 3组 | C. | 2组 | D. | 1组 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
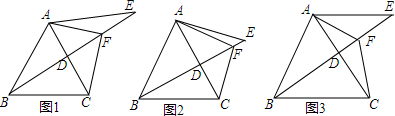
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
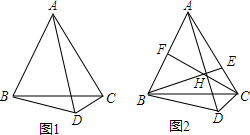
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{(-5)^{2}}=-5$ | B. | 4$\sqrt{3}$-$\sqrt{27}$=1 | C. | $\sqrt{18}÷\sqrt{2}$=9 | D. | $\sqrt{24}•\sqrt{\frac{3}{2}}=6$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
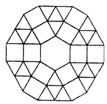 某广场地面图案的一部分如图所示,图案的中央是一块正六边形的地砖,周围用正三角形和正六边形的地砖密铺,环绕正六边形的那些正三角形和正方形为第一层,环绕第一层的那些正三角形和正方形为第二层,这样从里到外共铺了10层,每一层的外边界构成一个多边形,(注:多边形是由一些线段首尾顺次连接的封闭平面图形,各条线段是多边形的边;正六边形的各边长相等.)
某广场地面图案的一部分如图所示,图案的中央是一块正六边形的地砖,周围用正三角形和正六边形的地砖密铺,环绕正六边形的那些正三角形和正方形为第一层,环绕第一层的那些正三角形和正方形为第二层,这样从里到外共铺了10层,每一层的外边界构成一个多边形,(注:多边形是由一些线段首尾顺次连接的封闭平面图形,各条线段是多边形的边;正六边形的各边长相等.) 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com