
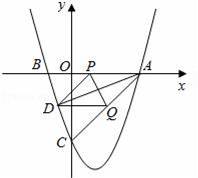
��ͼ�����κ���y=
 x2+bx+c��ͼ����x�ύ��A��3��0����B����1��0������y�ύ�ڵ�C������P��Qͬʱ��A�����������ÿ��1����λ���ȵ��ٶȷֱ���AB��AC���˶�������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶���
x2+bx+c��ͼ����x�ύ��A��3��0����B����1��0������y�ύ�ڵ�C������P��Qͬʱ��A�����������ÿ��1����λ���ȵ��ٶȷֱ���AB��AC���˶�������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶���
��1����ö��κ����Ľ���ʽ����C�����ꣻ
��2������P�˶���B��ʱ����Qֹͣ�˶�����ʱ����x�����Ƿ���ڵ�E��ʹ����A��E��QΪ�����������Ϊ���������Σ������ڣ������E�����ꣻ�������ڣ���˵�����ɣ�
��3����P��Q�˶���t��ʱ����APQ��PQ���ۣ���Aǡ��������������D�㴦�����ж���ʱ�ı���APDQ����״�������D�����꣮


�����㡿���κ����ۺ��⣮
��ר�⡿���������ۺ��⣻ѹ���⣮
����������1����A��B��������뺯��y=
 x2+bx+c�У����b��c�������������ʽ��C���꣮
x2+bx+c�У����b��c�������������ʽ��C���꣮
��2�����������������������AE=EQ��AQ=EQ��AE=AQ��������ֱƽ���ߣ���Բ��E����λ�ã���߳�Ϊx����ʾ�����ߺ����ù��ɶ�����E���꣮
��3��ע�P��Q�˶��ٶ���ͬ�����APQ�˶�ʱ��Ϊ���������Σ�����A��D�Գƣ���AP=DP��AQ=DQ�����ı����ı߶���ȣ������Σ��������ζԱ�ƽ������ȵ����ʿ���t��ʾD�����꣬��D��E�����ϣ����Դ��뼴����t������D�ɱ�ʾ��
����𡿷�����1����
�⣺��1���߶��κ���y=
 x2+bx+c��ͼ����x�ύ��A��3��0����B����1��0����
x2+bx+c��ͼ����x�ύ��A��3��0����B����1��0����
��
 ��
��
���
 ��
��
��y=
 x2��
x2��
 x��4��
x��4��
��C��0����4����
��2�����ڣ�
��ͼ1������Q��QD��OA��D����ʱQD��OC��


��A��3��0����B����1��0����C��0����4����O��0��0����
��AB=4��OA=3��OC=4��
��AC=
 =5��
=5��
�ߵ���P�˶���B��ʱ����Qֹͣ�˶���AB=4��
��AQ=4��
��QD��OC��
��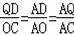
 ��
��
��
 ��
��
��QD=
 ��AD=
��AD=
 ��
��
����AQ�Ĵ�ֱƽ���ߣ���AO��E����ʱAE=EQ������AEQΪ���������Σ�


��AE=x����EQ=x��DE=AD��AE=|
 ��x|��
��x|��
����Rt��EDQ����
 ��x��2+��
��x��2+��
 ��2=x2����� x=
��2=x2����� x=
 ��
��
��OA��AE=3��
 =��
=��
 ��
��
��E����
 ��0����
��0����
˵����E��x��ĸ������ϣ�
����QΪԲ�ģ�AQ���뾶��Բ����x����E����ʱQE=QA=4��
��ED=AD=
 ��
��
��AE=
 ��
��
��OA��AE=3��
 =��
=��
 ��
��
��E����
 ��0����
��0����
�۵�AE=AQ=4ʱ��
1����E��A�����ʱ��
��OA��AE=3��4=��1��
��E����1��0����
2����E��A���ұ�ʱ��
��OA+AE=3+4=7��
��E��7��0����
�����������������������ĵ�E����E������Ϊ����
 ��0����
��0����
 ��0����1��0����7��0����
��0����1��0����7��0����
��3���ı���APDQΪ���Σ�D������Ϊ����
 ����
����
 �����������£�
�����������£�
��ͼ2��D�����PQ��A��Գƣ�����Q����FQ��AP��F��


��AP=AQ=t��AP=DP��AQ=DQ��
��AP=AQ=QD=DP��
���ı���AQDPΪ���Σ�
��FQ��OC��
��
 ��
��
��
 ��
��
��AF=
 ��FQ=
��FQ=
 ��
��
��Q��3��
 ����
����
 ����
����
��DQ=AP=t��
��D��3��
 ��t����
��t����
 ����
����
��D�ڶ��κ���y=
 x2��
x2��
 x��4�ϣ�
x��4�ϣ�
�ੁ
 =
=
 ��3��
��3��
 t��2��
t��2��
 ��3��
��3��
 t����4��
t����4��
��t=
 ����t=0����A�غϣ���ȥ����
����t=0����A�غϣ���ȥ����
��D����
 ����
����
 ����
����
��������
��1���ԣ�
��2���ߵ�P��Qͬʱ��A�����������ÿ��1����λ���ȵ��ٶȷֱ���AB��AC�˶�������Q��x�ᴹ�ߣ�����ΪH��
��A��3��0����C��0��4����
��lAC��y=
 x��4��
x��4��
�ߵ�P�˶���B��ʱ����Qֹͣ�˶���
��AP=AQ=4��
��QH=
 ��Qy=��
��Qy=��
 ��
��
����LAC��y=
 x��4�ã�Qx=
x��4�ã�Qx=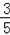
 ����Q��
����Q��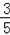
 ����
����
 ����
����
�ߵ�E��x���ϣ�
����E��a��0����
��A��3��0����Q��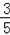
 ����
����
 ������AEQ����������
������AEQ����������
��AE=EQ��AE=AQ��EQ=AQ��
�ࣨa��3��2=��a��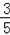
 ��2+��0+
��2+��0+
 ��2����a=��
��2����a=��
 ��
��
��a��3��2=��3��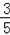
 ��2+��0+
��2+��0+
 ��2����a1=7��a2=��1��
��2����a1=7��a2=��1��
��a��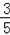
 ��2+��0+
��2+��0+
 ��2=��3��
��2=��3��
 ��2+��0+
��2+��0+
 ��2����a1=��
��2����a1=��
 ��a2=3���ᣩ
��a2=3���ᣩ
���E����������
 ��0����
��0����
 ��0����1��0����7��0����
��0����1��0����7��0����
��3����P��Q�˶���t�룬
����P��3��t��0����Q��3��
 t����
t����
 t����
t����
��KPQ=
 ��KPQ=��2��
��KPQ=��2��
��AD��PQ��
��KPQ•KAD=��1��
��KAD=
 ��
��
��A��3��0����
��lAD��y=
 x��
x��
 ��
��
��y=
 ��
��
��x1=3���ᣩ��x2=��
 ��
��
��D����
 ����
����
 ����
����
��DY=QY������
 t=��
t=��
 ��t=
��t=
 ��DQ��AP��DQ=AQ=AP����ʱ�ı���APDQ����״Ϊ���Σ�
��DQ��AP��DQ=AQ=AP����ʱ�ı���APDQ����״Ϊ���Σ�



�����������⿼���˶��κ������ʡ����ù��ɶ�����ֱ�������μ����ε�֪ʶ��������˵���⸴�ӵ�������ݶ��ܻ�������һ��ֵ����ϰ����Ŀ��


 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д� ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��ֱ��AB��CD�ཻ��O��OE��AB��O������1=2��2�����AOC�Ķ���Ϊ��������������


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�ھ���ABCD�У�AD=5��AB=3��AEƽ�֡�BAD��BC���ڵ�E�����߶�BE��EC�ij��ȷֱ�Ϊ��������


A��2��3 B��3��2 C��4��1 D��1��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ������������Χ��һ��ֱ�������Σ�64��400�ֱ�Ϊ���������ε��������ͼ����ĸ������������������ǣ�������


A��400+64 B��
 C��400��64 D��4002��642
C��400��64 D��4002��642
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
������ij��ѧΪ�˸�á�����ȫ���������С�����������Ա�У����ѧ���������飩������һ�����֪ʶ�˽�̶ȵĵ�����ԣ��ɼ���ΪA��B��C��D��E����飬x��ʾ���Գɼ�����ͨ���Բ��Գɼ��ķ������õ���ͼ��ʾ��������������ͳ��ͼ���������ͼ���ṩ����Ϣ����������⣺


��1���μӵ�����Ե�ѧ��Ϊ�������������ˣ�
��2��������ͳ��ͼ����������
��3�����ε�����Գɼ��е���λ���������������������ڣ�
��4�������Գɼ���80�����ϣ���80�֣�Ϊ���㣬����ѧ����ѧ��2600�ˣ���������������ݹ���ȫУѧ�����Գɼ�Ϊ�������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
������x��һԪ���η��̣�k��1��x2+2x��2=0����������ȵ�ʵ��������k��ȡֵ��Χ����������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ���ڵ�1����A1BC�У���B=20�㣬A1B=CB���ڱ�A1B����ȡһ��D���ӳ�CA1��A2��ʹA1A2=A1D���õ���2����A1A2D���ڱ�A2D����ȡһ��E���ӳ�A1A2��A3��ʹA2A3=A2E���õ���3����A2A3E������������������ȥ�����5������������A5Ϊ������ڽǶ�������������������
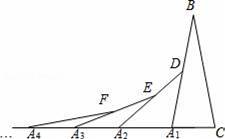

��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com