
如图,在平面直角坐标系 中,矩形
中,矩形 的边
的边 在
在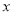 轴上,且
轴上,且 ,
,  ,直线
,直线 经过点
经过点 ,交
,交 轴于点
轴于点 .
.
(1)点 、
、 的坐标分别是
的坐标分别是 ( ),
( ), ( );
( );
(2)求顶点在直线 上且经过点
上且经过点 的抛物线的解析式;
的抛物线的解析式;
(3)将(2)中的抛物线沿直线 向上平移,平移后的抛物线交
向上平移,平移后的抛物线交 轴于点
轴于点 ,顶点为点
,顶点为点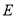 .求出当
.求出当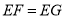 时抛物线的解析式.
时抛物线的解析式.

(1) C(4,2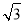 ),D(1,2
),D(1,2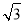 );(2)
);(2)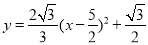 ;(3)y=
;(3)y=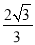 (x﹣
(x﹣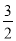 )2﹣
)2﹣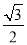 .
.
【解析】
试题分析:(1)根据题意可得点C的纵坐标为3,代入直线解析式可得出点C的横坐标,继而也可得出点D的坐标;
(2)由题意可得点C和点D关于抛物线的对称轴对称,从而得出抛物线的对称轴为x=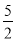 ,再由抛物线的顶点在直线y=
,再由抛物线的顶点在直线y=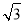 x?2
x?2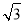 上,可得出顶点坐标为(
上,可得出顶点坐标为(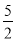 ,
,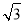 ),设出顶点式,代入点C的坐标即可得出答案.
),设出顶点式,代入点C的坐标即可得出答案.
试题解析:(1)C(4,2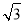 ),D(1,2
),D(1,2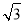 )
)
(2)由二次函数对称性得,顶点横坐标为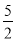 ,
,
令x=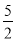 ,则
,则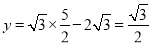 ,
,
∴顶点坐标为(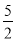 ,
,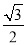 ),
),
∴设抛物线解析式为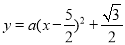 ,把点D(1,
,把点D(1,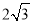 )代入得,
)代入得,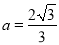
∴解析式为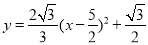
(3)设顶点E在直线上运动的横坐标为m,则E(m,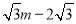 )
)
∴可设解析式为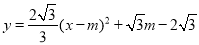 ,
,
当GE=EF时,FG=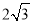 m,则F(0,
m,则F(0,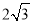 m﹣
m﹣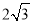 ),
),
代入解析式得: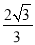 m2+
m2+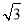 m﹣
m﹣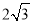 =
=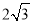 m﹣
m﹣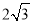 ,
,
解得m=0(舍去),m=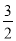 ,
,
此时所求的解析式为:y=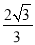 (x﹣
(x﹣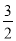 )2﹣
)2﹣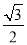
考点:二次函数综合题.


科目:初中数学 来源:2013-2014学年江苏省无锡市九年级二模数学试卷(解析版) 题型:解答题
如图①,将□ABCD置于直角坐标系中,其中BC边在x轴上(B在C的左边),点D坐标为(0,4),直线MN: 沿着x轴的负方向以每秒1个单位的长度平移,设在平移过程中该直线被□ABCD截得的线段长度为m,平移时间为t,m与t的函数图像如图②所示.
沿着x轴的负方向以每秒1个单位的长度平移,设在平移过程中该直线被□ABCD截得的线段长度为m,平移时间为t,m与t的函数图像如图②所示.
(1)填空:点C的坐标为 ;
在平移过程中,该直线先经过B、D中的哪一点? ;(填“B”或“D”)
(2)点B的坐标为 ,n= ,a= ;
(3)求图②中线段EF的解析式;
(4)t为何值时,该直线平分□ABCD的面积?

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市九年级二模数学试卷(解析版) 题型:选择题
如图,在斜边为3的等腰直角三角形OAB中,作内接正方形A1B1C1D1;在等腰直角三角形OA1B1中,作内接正方形A2B2C2D2;在等腰直角三角形OA2B2中,作内接正方形A3B3C3D3…依次作下去,则第2014个正方形A2014B2014C2014D2014的边长是( )

A.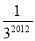 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市九年级二模数学试卷(解析版) 题型:选择题
若一个正多边形的一个外角是45°,则这个正多边形的边数是 ( )
A.7 B.8 C.9 D.10
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市锡山区九年级下学期期中考试(一模)数学试卷(解析版) 题型:解答题
如图,四边形ABCD是菱形,点E在BC上, ,试在AE上确定一点G,使△ABG≌△DAF.请你写出两种确定点G的方案,并就其中一种方案的具体作法证明△ABG≌△DAF.
,试在AE上确定一点G,使△ABG≌△DAF.请你写出两种确定点G的方案,并就其中一种方案的具体作法证明△ABG≌△DAF.
方案一:作法: ;
方案二:(1)作法: .
(2)证明:

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市锡山区九年级下学期期中考试(一模)数学试卷(解析版) 题型:填空题
如图是一张简易活动餐桌,现测得OA=OB=30cm,OC=OD=50cm,现要求桌面离地面的高度为40cm,那么两条桌腿的张角∠COD的大小应为 .

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市九年级4月高效课堂调研数学试卷(解析版) 题型:填空题
截至2013年12月31日,余额宝规模已达到1853亿元,这个数据用科学记数法可表示为 元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com