
【题目】如图,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.
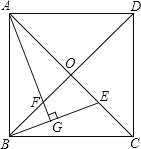
(1)试说明OE=OF;
(2)当AE=AB时,过点E作EH⊥BE交AD边于H,找出与△AHE全等的一个三角形加以证明,
(3)在(2)的条件下若该正方形边长为1,求AH的长.
【答案】(1)证明解解析(2)答案见解析(3)![]() ﹣1
﹣1
【解析】
试题分析:(1)根据正方形性质得出AC⊥BD,OA=OB,求出∠FAO=∠EBO,根据ASA推出△AFO≌△BEO即可;
(2)根据正方形性质得出∠ACB=∠DAC=45°,∠ABE+∠EBC=90°,求出∠CBE=∠AEH,AE=AB=BC,证△BCE≌△EAH;
(3)根据全等三角形的性质推出CE=AH,即可得出答案.
(1)解:∵四边形ABCD是正方形,
∴AC⊥BD,OA=OB,
∴∠AOF=∠BOE=90°,
∵AG⊥BE,
∴∠FGB=90°,
∴∠OBE+∠BFG=90°,∠FAO+∠AFO=90°,
∵∠AFO=∠BFG,
∴∠FAO=∠EBO,
在△AFO和△BEO中,
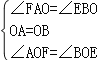 ,
,
∴△AFO≌△BEO(ASA),
∴OE=OF.

(2)△BCE≌△EAH,
证明:∵四边形ABCD是正方形,
∴∠ACB=∠DAC=45°,∠ABE+∠EBC=90°,
∵EH⊥BE,
∴∠AEH+∠AEB=90°,
∵AE=AB,
∴∠ABE=∠AEB,
∴∠CBE=∠AEH,
∵AE=AB=BC,
在△BCE和△EAH中,
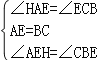 ,
,
∴△BCE≌△EAH(ASA);
(3)解:∵△BCE≌△EAH,
∴CE=AH,
∵AB=BC=1,
∴AC=![]() ,
,
∵AE=AB=1,
∴AH=CE=AC﹣AE=![]() ﹣1.
﹣1.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
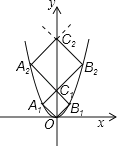
【题目】如图,已知点A1,A2,…,A2011在函数y=x2位于第二象限的图象上,点B1,B2,…,B2011在函数y=x2位于第一象限的图象上,点C1,C2,…,C2011在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2010A2011C2011B2011都是正方形,则正方形C2010A2011C2011B2011的边长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由二次函数y=2(x﹣3)2+1可知( )
A.其图象的开口向下
B.其图象的对称轴为x=﹣3
C.其最大值为1
D.当x<3时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某气球内充满一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
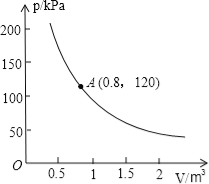
(1)写出这一函数的表达式.
(2)当气体体积为1 m3时,气压是多少?
(3)当气球内的气压大于140 kPa时,气球将爆炸,为了安全起见,气体的体积应不大于多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】保护水资源,人人有责,我国是缺水国家,目前可利用淡水资源总量仅约为899000亿立方米,899000亿用科学记数法表示为( )
A.8.99×1013 B.0.899×1014 C.8.99×1012 D.89.9×1011
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com