
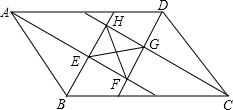
 如图,在?ABCD中,四个内角的平分线分别相交于点E,F,G,H.
如图,在?ABCD中,四个内角的平分线分别相交于点E,F,G,H.分析 (1)EG=FH;
(2)因为平行四边形的邻角互补,则邻角的平分线组成的角为90°,有三个角是90°的四边形是矩形,故EG=FH.
解答 (1)解:EG=FH.
故答案为EG=FH. (2)证明:∵四边形ABCD是平行四边形,
(2)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠BAD+∠ABC=180°.
又∵AF,BH分别平分∠BAD,∠ABC,
∴∠BAE=$\frac{1}{2}$∠BAD,∠ABE=$\frac{1}{2}$∠ABC,
∴∠BAE+∠ABE=90°,
∴∠AEB=90°,
∴∠FEH=90°.
同理可证∠EFG=90°,∠EHG=90°,
∴四边形EFGH为矩形,
∴EG=FH.
点评 本题考查了矩形的判定,平行四边形的性质,角平分线的定义,平行线的性质,难度适中.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:填空题
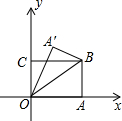 如图,四边形0ABC为矩形,A在x轴上,C在y轴上,B点坐标为(4,3),将△OAB沿OB翻折,A的对应点为A′,0A′交BC于D,则D点的坐标为($\frac{7}{8}$,3).
如图,四边形0ABC为矩形,A在x轴上,C在y轴上,B点坐标为(4,3),将△OAB沿OB翻折,A的对应点为A′,0A′交BC于D,则D点的坐标为($\frac{7}{8}$,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
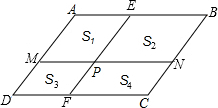 如图,在平行四边形ABCD中.AB∥CD,AD∥BC,P为平行四边形ABCD内一点,过P作EF∥BC,MN∥CD,设四边形AMPE、四边形EPNB、四边形MDFP、四边形CFPN的面积分别为S1、S2、S3、S4.
如图,在平行四边形ABCD中.AB∥CD,AD∥BC,P为平行四边形ABCD内一点,过P作EF∥BC,MN∥CD,设四边形AMPE、四边形EPNB、四边形MDFP、四边形CFPN的面积分别为S1、S2、S3、S4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
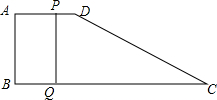 如图,在四边形ABCD中,AD∥BC,且AD<BC,AD=10cm,AB=12cm,BC=18cm,CD=15cm,动点P,Q分别从点A、C同时出发,点P以2cm/s的速度由点A向点B运动,点Q以3cm/s的速度由点C向点B运动.
如图,在四边形ABCD中,AD∥BC,且AD<BC,AD=10cm,AB=12cm,BC=18cm,CD=15cm,动点P,Q分别从点A、C同时出发,点P以2cm/s的速度由点A向点B运动,点Q以3cm/s的速度由点C向点B运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com