
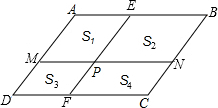
 ��ͼ����ƽ���ı���ABCD�У�AB��CD��AD��BC��PΪƽ���ı���ABCD��һ�㣬��P��EF��BC��MN��CD�����ı���AMPE���ı���EPNB���ı���MDFP���ı���CFPN������ֱ�ΪS1��S2��S3��S4��
��ͼ����ƽ���ı���ABCD�У�AB��CD��AD��BC��PΪƽ���ı���ABCD��һ�㣬��P��EF��BC��MN��CD�����ı���AMPE���ı���EPNB���ı���MDFP���ı���CFPN������ֱ�ΪS1��S2��S3��S4������ ��1������ƽ�й��������ۼ��ɵõ����ۣ�
��2����E��EH��CD��H������ƽ���ı��ε��ж��õ��ı���AMPE��EPNB��ƽ���ı��Σ���ƽ���ı��ε������ʽ���ɵõ����ۣ�
��3��������֪�����õ��ı���AMPE��EPNB��MPFD��PFCN��ƽ���ı��Σ���ƽ���ı��ε�����õ�$\frac{{S}_{1}}{{S}_{2}}$=$\frac{{S}_{3}}{{S}_{4}}$�����ɵõ����ۣ�
���  �⣺��1��MN��ABƽ�У�
�⣺��1��MN��ABƽ�У�
���ɣ���AB��CD��MN��CD��
��MN��AB��
��2��$\frac{{S}_{1}}{{S}_{2}}$��$\frac{MP}{NP}$��ȣ�
���ɣ���E��EH��CD��H��
��CD��MN��
��EG��MN��
��AB��MN��AD��EF��BC��
���ı���AMPE��EPNB��ƽ���ı��Σ�
��$\frac{{S}_{1}}{{S}_{2}}$=$\frac{PM•EG}{PN•EG}$=$\frac{MP}{NP}$��
��3��S1•S4=S2•S3��
��AB��MN��CD��AD��EF��BC����
���ı���AMPE��EPNB��MPFD��PFCN��ƽ���ı��Σ�
��$\frac{{S}_{1}}{{S}_{2}}$=$\frac{PM•EG}{PN•EG}$=$\frac{MP}{NP}$��$\frac{{S}_{3}}{{S}_{4}}$=$\frac{PM•GH}{PN•GH}$=$\frac{PM}{PN}$��
��$\frac{{S}_{1}}{{S}_{2}}$=$\frac{{S}_{3}}{{S}_{4}}$��
��S1•S4=S2•S3��
���� ���⿼����ƽ���ı��ε��ж������ʣ�ƽ���ı��ε�����ļ��㣬��������ƽ���ı��ε����ʶ����ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
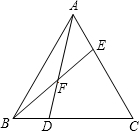 ��ͼ����֪��ABC�У�AE��EC=1��3��BD��DC=1��2��AD��BE���ڵ�F����$\frac{EF}{BF}$+$\frac{AF}{DF}$��ֵ��
��ͼ����֪��ABC�У�AE��EC=1��3��BD��DC=1��2��AD��BE���ڵ�F����$\frac{EF}{BF}$+$\frac{AF}{DF}$��ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
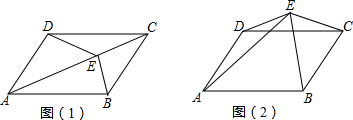
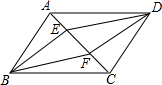 ��ͼ����?ABCD�У���E��F�ĶԽ���AC�ϵ����㣬��AE=CF����֤��DE=BF��BE=DF��
��ͼ����?ABCD�У���E��F�ĶԽ���AC�ϵ����㣬��AE=CF����֤��DE=BF��BE=DF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
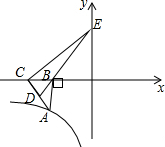 ��ͼ��Rt��ABC��ֱ�DZ�BC��x�Ḻ�����ϣ�б��AC�ϵ�����BD�ķ����ӳ��߽�y���������ڵ�E��˫����y=$\frac{k}{x}$��x��0����ͼ����A��S��BEC=8����k=16��
��ͼ��Rt��ABC��ֱ�DZ�BC��x�Ḻ�����ϣ�б��AC�ϵ�����BD�ķ����ӳ��߽�y���������ڵ�E��˫����y=$\frac{k}{x}$��x��0����ͼ����A��S��BEC=8����k=16���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
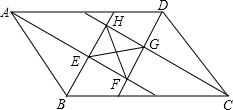 ��ͼ����?ABCD�У��ĸ��ڽǵ�ƽ���߷ֱ��ཻ�ڵ�E��F��G��H��
��ͼ����?ABCD�У��ĸ��ڽǵ�ƽ���߷ֱ��ཻ�ڵ�E��F��G��H���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
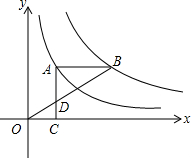 ��ͼ����A��˫����y=$\frac{2}{x}$�ϣ���B��˫����y=$\frac{k}{x}$��k��0���ϣ�AB��x�ᣬ����A��AC��x����C������OB��AC�ཻ�ڵ�D����AD=2DC����k��ֵΪ6��
��ͼ����A��˫����y=$\frac{2}{x}$�ϣ���B��˫����y=$\frac{k}{x}$��k��0���ϣ�AB��x�ᣬ����A��AC��x����C������OB��AC�ཻ�ڵ�D����AD=2DC����k��ֵΪ6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ�������������ÿ��С�����εı߳���Ϊ1��ÿ��С�����εĶ��������㣬������Ҫ������
��ͼ�������������ÿ��С�����εı߳���Ϊ1��ÿ��С�����εĶ��������㣬������Ҫ�������鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com