
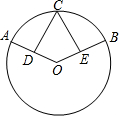
 如图,在⊙O中,点C是$\widehat{AB}$的中点,D、E分别是半径OA和OB的中点,求证:CD=CE.
如图,在⊙O中,点C是$\widehat{AB}$的中点,D、E分别是半径OA和OB的中点,求证:CD=CE. 分析 连接OC,构建全等三角形△COD和△COE;然后利用全等三角形的对应边相等证得CD=CE.
解答 证明:连接CO,如图所示,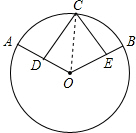
∵OA=OB,且D、E分别是半径OA和OB的中点,
∴OD=OE,
又∵点C是$\widehat{AB}$的中点,
∴$\widehat{AC}$=$\widehat{CB}$,
∴∠COD=∠COE,
在△COD和△COE中,
$\left\{\begin{array}{l}{OC=OC}\\{∠COD=∠COE}\\{OD=OE}\end{array}\right.$,
∴△COD≌△COE(SAS),
∴CD=CE.
点评 本题考查了圆心角、弧、弦的关系,以及全等三角形的判定与性质.判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2015年元旦前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
2015年元旦前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销,经过调查,得到如下数据:| 销售单价x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量y(件) | … | 500 | 400 | 300 | 200 | 100 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
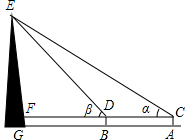 如图,小嘉利用测角仪测量塔高,他分别站在A、B两点测得塔顶的仰角α=45°,β=50°.AB为10米.已知小嘉的眼睛距地面的高度AC为1.5米,计算塔的高度.(参考数据:sin50°取0.8,cos50°取0.6,tan50°取1.2)
如图,小嘉利用测角仪测量塔高,他分别站在A、B两点测得塔顶的仰角α=45°,β=50°.AB为10米.已知小嘉的眼睛距地面的高度AC为1.5米,计算塔的高度.(参考数据:sin50°取0.8,cos50°取0.6,tan50°取1.2)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com