
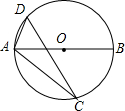
 如图,AB为⊙0的直径,点C、D在⊙0上,且∠ADC=52°,则∠BAC=38°.
如图,AB为⊙0的直径,点C、D在⊙0上,且∠ADC=52°,则∠BAC=38°.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 若直线y=-kx-2过第一、三、四象限,则k<0 | |
| B. | 三角形三条角平分线的交点到三个顶点的距离相等 | |
| C. | 如果∠A=∠B,那么∠A和∠B是对顶角 | |
| D. | 如果a•b=0,那么a=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1-$\frac{1}{{{2^{2015}}}}$ | B. | $\frac{2014}{2015}$ | C. | 1-$\frac{1}{{{2^{2014}}}}$ | D. | $\frac{2013}{2014}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
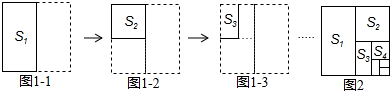
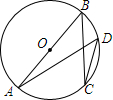 如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )
如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )| A. | $\frac{{8\sqrt{13}}}{3}$ | B. | $\frac{16}{3}$ | C. | $\frac{{24\sqrt{5}}}{5}$ | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
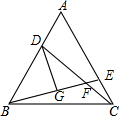 已知,如图,在等边三角形ABC中,点D,E分别在AB,AC边上,AD=CE,CD与BE交于F,DG⊥BE,求证:
已知,如图,在等边三角形ABC中,点D,E分别在AB,AC边上,AD=CE,CD与BE交于F,DG⊥BE,求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 中秋节期间,某商场为了吸引顾客,开展有奖促销活动,设立了一个可以自由转动的转盘,转盘被分成三个面积相等的扇形,三个扇形区域里分别标有“10元”、“20元”、“30元”的字样(如图).规定:同一天内,顾客在本商场每消费满100元,就可以转动转盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券.某顾客当天消费240元,转了两次转盘.
中秋节期间,某商场为了吸引顾客,开展有奖促销活动,设立了一个可以自由转动的转盘,转盘被分成三个面积相等的扇形,三个扇形区域里分别标有“10元”、“20元”、“30元”的字样(如图).规定:同一天内,顾客在本商场每消费满100元,就可以转动转盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券.某顾客当天消费240元,转了两次转盘.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com