
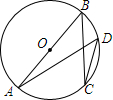
 如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )
如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )| A. | $\frac{{8\sqrt{13}}}{3}$ | B. | $\frac{16}{3}$ | C. | $\frac{{24\sqrt{5}}}{5}$ | D. | 12 |
科目:初中数学 来源: 题型:解答题
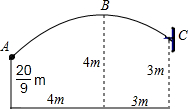 一场篮球赛中,球员甲跳起投篮,已知球在A处出手时离地面$\frac{20}{9}$m,与篮筐中心C的水平距离为7m,当球运行的水平距离是4m时,达到最大高度4m(B处),篮筐距地面3m,篮球运行的路线为抛物线(如图所示).
一场篮球赛中,球员甲跳起投篮,已知球在A处出手时离地面$\frac{20}{9}$m,与篮筐中心C的水平距离为7m,当球运行的水平距离是4m时,达到最大高度4m(B处),篮筐距地面3m,篮球运行的路线为抛物线(如图所示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
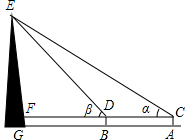 如图,小嘉利用测角仪测量塔高,他分别站在A、B两点测得塔顶的仰角α=45°,β=50°.AB为10米.已知小嘉的眼睛距地面的高度AC为1.5米,计算塔的高度.(参考数据:sin50°取0.8,cos50°取0.6,tan50°取1.2)
如图,小嘉利用测角仪测量塔高,他分别站在A、B两点测得塔顶的仰角α=45°,β=50°.AB为10米.已知小嘉的眼睛距地面的高度AC为1.5米,计算塔的高度.(参考数据:sin50°取0.8,cos50°取0.6,tan50°取1.2)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
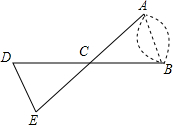 如图,A、B两点分别位于一个假山两边,请你利用全等三角形的知识设计一种测量A、B间距离的方案,并说明其中的道理.
如图,A、B两点分别位于一个假山两边,请你利用全等三角形的知识设计一种测量A、B间距离的方案,并说明其中的道理.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com