
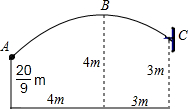
 一场篮球赛中,球员甲跳起投篮,已知球在A处出手时离地面$\frac{20}{9}$m,与篮筐中心C的水平距离为7m,当球运行的水平距离是4m时,达到最大高度4m(B处),篮筐距地面3m,篮球运行的路线为抛物线(如图所示).
一场篮球赛中,球员甲跳起投篮,已知球在A处出手时离地面$\frac{20}{9}$m,与篮筐中心C的水平距离为7m,当球运行的水平距离是4m时,达到最大高度4m(B处),篮筐距地面3m,篮球运行的路线为抛物线(如图所示).分析 (1)建立适当的平面直角坐标系,根据已知条件即可得到结论;
(2)根据(1)中的篮球运动抛物线的解析式,把坐标(7,3)代入判断是否满足,则即可确定篮球是否能准确投中.
解答 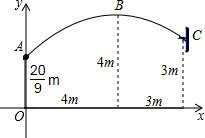 解:(1)过A作水平线的垂线,垂直为O,以O为坐标原点,直线OA为y轴,建立平面直角坐标系,由题意得A(0,$\frac{20}{9}$),顶点B(4,4),
解:(1)过A作水平线的垂线,垂直为O,以O为坐标原点,直线OA为y轴,建立平面直角坐标系,由题意得A(0,$\frac{20}{9}$),顶点B(4,4),
设抛物线的解析式为y=a(x-4)2+4,
∴$\frac{20}{9}$=a(x-4)2+4.
解得:a=-$\frac{1}{9}$.
∴抛物线的解析式为:y=-$\frac{1}{9}$(x-4)2+4;
(2)当x=7时,y=-$\frac{1}{9}$(7-4)2+4=3,
∵点(7,3)在抛物线上,
∴球能准确投中.
点评 本题考查了二次函数在实际生活中的应用,待定系数法求函数的解析式,正确的求得函数的解析式是解题的关键.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:选择题
| A. | sinA=$\frac{2}{3}$ | B. | cosA=$\frac{2}{3}$ | C. | tanA=$\frac{2}{3}$ | D. | cotA=$\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1-$\frac{1}{{{2^{2015}}}}$ | B. | $\frac{2014}{2015}$ | C. | 1-$\frac{1}{{{2^{2014}}}}$ | D. | $\frac{2013}{2014}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
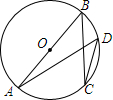 如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )
如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )| A. | $\frac{{8\sqrt{13}}}{3}$ | B. | $\frac{16}{3}$ | C. | $\frac{{24\sqrt{5}}}{5}$ | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某水池的容积为90m3,水池中已有水10m3,现按8m3/h的流量向水池中注水.
某水池的容积为90m3,水池中已有水10m3,现按8m3/h的流量向水池中注水.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com