
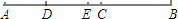 如图,已知点C为AB上一点,AC=24cm,CB=$\frac{2}{3}$AC,D、E分别为AC、AB的中点,求DE的长.
如图,已知点C为AB上一点,AC=24cm,CB=$\frac{2}{3}$AC,D、E分别为AC、AB的中点,求DE的长. 分析 先求得BC=16cm,从而可求得AB=40cm,然后由中点的定义求得AD=$\frac{1}{2}AC$=12cm,AE=$\frac{1}{2}AB$=20cm,最后由DE=AE-AD求解即可.
解答 解:∵AC=24cm,CB=$\frac{2}{3}$AC,
∴BC=$\frac{2}{3}×24$=16cm.
∴AB=AC+CB=24+16=40cm.
∵D是AC的中点,
∴AD=$\frac{1}{2}AC$=12cm.
∵E是AC的中点,
∴AE=$\frac{1}{2}AB$=20cm.
∴DE=AE-AD=20-12=8cm.
∴DE的长为8cm.
点评 本题主要考查的是两点间的距离,求得AD、AE的长是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | $y=\frac{1}{3}{x^2}$ | B. | $y=3{x^2}+\frac{1}{3}$ | C. | $y={({x+\frac{1}{3}})^2}$ | D. | $y={({x-\frac{1}{3}})^2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
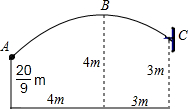 一场篮球赛中,球员甲跳起投篮,已知球在A处出手时离地面$\frac{20}{9}$m,与篮筐中心C的水平距离为7m,当球运行的水平距离是4m时,达到最大高度4m(B处),篮筐距地面3m,篮球运行的路线为抛物线(如图所示).
一场篮球赛中,球员甲跳起投篮,已知球在A处出手时离地面$\frac{20}{9}$m,与篮筐中心C的水平距离为7m,当球运行的水平距离是4m时,达到最大高度4m(B处),篮筐距地面3m,篮球运行的路线为抛物线(如图所示).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
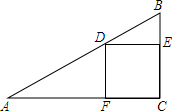 正方形CEDF的顶点D、E、F分别在△ABC的边AB、BC、AC上.
正方形CEDF的顶点D、E、F分别在△ABC的边AB、BC、AC上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
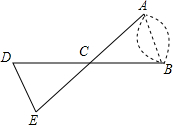 如图,A、B两点分别位于一个假山两边,请你利用全等三角形的知识设计一种测量A、B间距离的方案,并说明其中的道理.
如图,A、B两点分别位于一个假山两边,请你利用全等三角形的知识设计一种测量A、B间距离的方案,并说明其中的道理.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com