
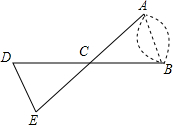
 如图,A、B两点分别位于一个假山两边,请你利用全等三角形的知识设计一种测量A、B间距离的方案,并说明其中的道理.
如图,A、B两点分别位于一个假山两边,请你利用全等三角形的知识设计一种测量A、B间距离的方案,并说明其中的道理.分析 (1)先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至E,BC至D,使EC=AC,DC=BC,最后测出DE的距离即为AB的长;
(2)利用SAS证明△EDC≌△ABC,根据全等三角形的对应边相等得到ED=AB.
解答 解:(1)测量方案:先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至E,BC至D,使EC=AC,DC=BC,最后测出DE的距离即为AB的长;
(2)理由:
在△EDC和△ABC中,
$\left\{\begin{array}{l}{EC=AC}\\{∠DCE=∠BCA}\\{DC=BC}\end{array}\right.$,
∴△EDC≌△ABC(SAS),
∴ED=AB(全等三角形对应边相等),
即DE的距离即为AB的长.
点评 本题考查了全等三角形的应用;解答本题的关键是设计三角形全等,巧妙地借助两个三角形全等,寻找所求线段与已知线段之间的等量关系.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | a•x%元 | B. | a(1+x%)元 | C. | $\frac{a}{x%}$元 | D. | $\frac{a}{1-x%}$元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1-$\frac{1}{{{2^{2015}}}}$ | B. | $\frac{2014}{2015}$ | C. | 1-$\frac{1}{{{2^{2014}}}}$ | D. | $\frac{2013}{2014}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
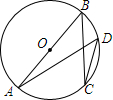 如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )
如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )| A. | $\frac{{8\sqrt{13}}}{3}$ | B. | $\frac{16}{3}$ | C. | $\frac{{24\sqrt{5}}}{5}$ | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
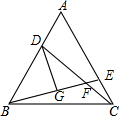 已知,如图,在等边三角形ABC中,点D,E分别在AB,AC边上,AD=CE,CD与BE交于F,DG⊥BE,求证:
已知,如图,在等边三角形ABC中,点D,E分别在AB,AC边上,AD=CE,CD与BE交于F,DG⊥BE,求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某水池的容积为90m3,水池中已有水10m3,现按8m3/h的流量向水池中注水.
某水池的容积为90m3,水池中已有水10m3,现按8m3/h的流量向水池中注水.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是一张关于340万年前地球表层的照片,340万用科学记数法表示为( )
如图是一张关于340万年前地球表层的照片,340万用科学记数法表示为( )| A. | 3.40×102 | B. | 340×104 | C. | 3.40×104 | D. | 3.40×106 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com