
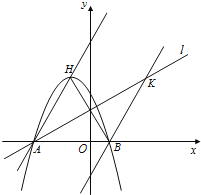
【题目】如图,抛物线y=mx![]() +2mx-3m(m≠0)的顶点为H,与
+2mx-3m(m≠0)的顶点为H,与![]() 轴交于A、B两点(B点在A点右侧),点H、B关于直线l:
轴交于A、B两点(B点在A点右侧),点H、B关于直线l:![]() 对称,过点B作直线BK∥AH交直线l于K点.
对称,过点B作直线BK∥AH交直线l于K点.
(1)求A、B两点坐标,并证明点A在直线I上。
(2)求此抛物线的解析式;
(3)将此抛物线向上平移,当抛物线经过K点时,设顶点为N,求出NK的长.
【答案】(1) A(-3,0) B(1,0) ; (2)y=-![]() x
x![]() -
-![]() x+
x+![]() ; (3)NK=4
; (3)NK=4![]()
【解析】
(1)令y=0,解关于x的一元二次方程,即可得到点A、B的坐标;然后把点A的坐标代入直线l的解析式,计算即可证明点A在直线上;
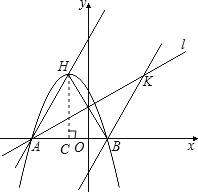
(2)根据轴对称的性质可得AH=AB,根据直线l的解析式求出直线l与x轴的夹角为30°,然后得到∠HAB的度数是60°,过点H作HC⊥x轴于点C,然后解直角三角形求出AC、HC,从而得到OC的长度,然后写出点H的坐标,再把点H的坐标代入抛物线解析式计算求出m的值,即可得解;
(3)根据平行直线的解析式的k值相等求出直线BK的解析式的k值,然后利用待定系数法求出直线BK的解析式,与直线l的解析式联立求解得到点K的值,再利用抛物线解析式求出相应横坐标上的点,从而求出抛物线向上移动的距离,然后得到平移后的抛物线的顶点N的坐标,根据两点间的距离公式计算即可得到NK的值.
令y=0,则mx2+2mx-3m=0(m≠0),
解得x1=-3,x2=1,
∵B点在A点右侧,
∴A点坐标为(-3,0),B点坐标为(1,0),
证明:∵直线l:![]()
当x=-3时,![]()
∴点A在直线l上;
(2)∵点H、B关于过A点的直线l:![]() 对称,
对称,
∴AH=AB=4,
设直线l与x轴的夹角为α,则![]()
所以,∠α=30°,
∴∠HAB=60°,
过顶点H作HC⊥AB交AB于C点,
则![]()
∴顶点H![]()
代入抛物线解析式,得![]()
解得m=-![]()
所以,抛物线解析式为![]()
(3)∵BK∥AH
∴直线BK的k=tan60°=![]()
设直线BK的解析式为y=![]() x+b,
x+b,
∵B点坐标为(1,0),
∴![]() +b=0,
+b=0,
解得b=-![]() ,
,
∴直线BK的解析式为y=![]() x-
x-![]()
联立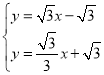
解得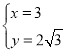
∴点K的坐标为(3,2![]() ),
),
当x=3时,![]()
∴平移后与点K重合的点的坐标为(3,-6![]() ),
),
平移距离为2![]() -(-6
-(-6![]() )=8
)=8![]() ,
,
∵平移前顶点坐标为(-1,2![]() ),
),
2![]() +8
+8![]() =10
=10![]() ,
,
∴平移后顶点坐标N(-1,10![]() ),
),
![]()
所以,NK的长是4![]()


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连接AA1,CC1.若△ABA1的面积为4,求△CBC1的面积;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,求线段EP1长度的最大值与最小值.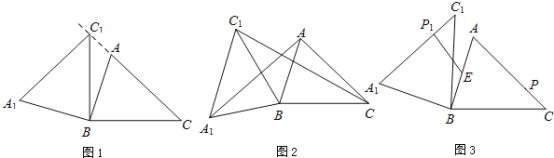
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备购买若干台A型电脑和B型打印机.如果购买1台A型电脑,2台B型打印机,一共需要花费5900元;如果购买2台A型电脑,2台B型打印机,一共需要花费9400元.
(1)求每台A型电脑和每台B型打印机的价格分别是多少元?
(2)如果学校购买A型电脑和B型打印机的预算费用不超过20000元,并且购买B型打印机的台数要比购买A型电脑的台数多1台,那么该学校至多能购买多少台B型打印机?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
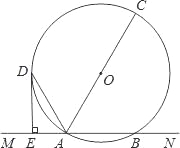
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中是小明完成的一道作业题,请你参考小明的解答方法解答下面的问题:
小明的作业
计算:(-4)7×0.257
解:(-4)7×0.257=(-4×0.25)7
=(-1)7
=-1
(1)计算①82018×(-0.125)2018② ![]()
(2)看2·4n·16n=219 , 求n的值
查看答案和解析>>
科目:初中数学 来源: 题型:
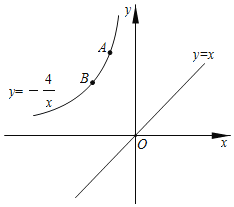
【题目】如图,反比例函数y=﹣![]() 在第二象限的图象上有两点A、B,它们的横坐标分别为﹣1、﹣2,在直线y=x上求一点P,使PA+PB最小.则P点坐标为( )
在第二象限的图象上有两点A、B,它们的横坐标分别为﹣1、﹣2,在直线y=x上求一点P,使PA+PB最小.则P点坐标为( )
A. P(![]() ,
,![]() )B. P(
)B. P(![]() ,
,![]() )C. P(1,1)D. P(
)C. P(1,1)D. P(![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3BC,以点A为圆心,AD为半径画弧交AB于点E连接CE,作线段CE的中垂线交AB于点F,连接CF,则sin∠CFB=_____.
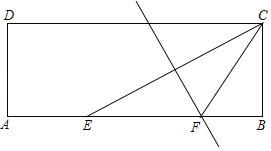
查看答案和解析>>
科目:初中数学 来源: 题型:
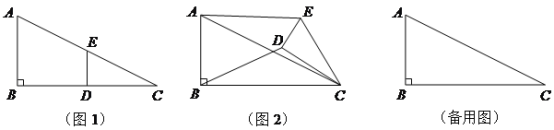
【题目】(10分)如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE. 将△EDC绕点C按顺时针方向旋转,记旋转角为α.
(1)问题发现
① 当![]() 时,
时,![]() ;② 当
;② 当![]() 时,
时,![]()
(2)拓展探究
试判断:当0°≤α<360°时,![]() 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明.
(3)问题解决
当△EDC旋转至A、D、E三点共线时,直接写出线段BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com