
【题目】填空,完成下列说理过程
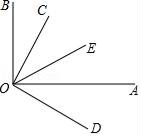
如图,∠AOB=90°,∠COD=90°,OA平分∠DOE,若∠BOC=20°,求∠COE的度数
解:因为∠AOB=90°.
所以∠BOC+∠AOC=90°
因为∠COD=90°
所以∠AOD+∠AOC=90°.
所以∠BOC=∠AOD. ( )
因为∠BOC=20°.
所以∠AOD=20°.
因为OA平分∠DOE
所以∠ =2∠AOD= °. ( )
所以∠COE=∠COD﹣∠DOE= °
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy,直线y=x﹣1与y轴交于点A,与双曲线y= ![]() 交于点B(m,2).
交于点B(m,2).
(1)求点B的坐标及k的值;
(2)将直线AB平移,使它与x轴交于点C,与y轴交于点D,若△ABC的面积为6,求直线CD的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
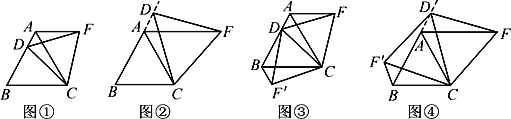
【题目】(1)操作发现:如图①,D是等边△ABC的边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF,你能发现AF与BD之间的数量关系吗?并证明你发现的结论;
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与B不重合),连接DC,以DC为边在BC上方和下方分别作等边△DCF和等边△DCF′,连接AF,BF′,探究AF,BF′与AB有何数量关系?并证明你的探究的结论;Ⅱ.如图④,当动点D在等边△ABC的边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司到果园基地购买某种优质水果,慰问医务工作者,果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案,甲方案:每千克9元,由基地送货上门.乙方案:每千克8元,由顾客自己租车运回,已知该公司租车从基地到公司的运输费为5000元.
(1)分别写出该公司两种购买方案的付款y(元)与所购买的水果质量x(千克)之间的函数关系式,并写出自变量x的取值范围.
(2)依据购买量判断,选择哪种购买方案付款最少?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某“数学兴趣小组”根据学习函数的经验,对函数y= ![]() 的图象和性质进行了探究,探究过程如下,请补充完整:
的图象和性质进行了探究,探究过程如下,请补充完整: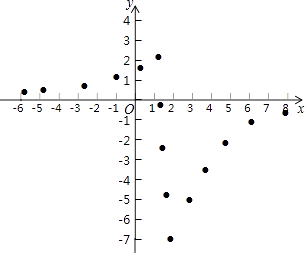
(1)该函数的自变量x的取值范围是;
(2)同学们先找到y与x的几组对应值,然后在下图的平面直角坐标系xOy中,描出各对对应值为坐标的点.请你根据描出的点,画出该函数的图象;
(3)结合画出的函数图象,写出该函数的一条性质: .
查看答案和解析>>
科目:初中数学 来源: 题型:
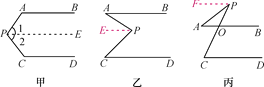
【题目】阅读下列解答过程:(1)如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
(2)如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为 ![]() ,BD是⊙O的切线,D为切点,过圆上一点C作BD的垂线,垂足为B,BC=3,点A是优弧CD的中点,则sin∠A的值是( )
,BD是⊙O的切线,D为切点,过圆上一点C作BD的垂线,垂足为B,BC=3,点A是优弧CD的中点,则sin∠A的值是( ) 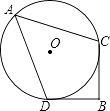
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(1, ![]() ),点B(2,0),P为线段OB上一点,过点P作PQ∥OA,交AB于点Q,连接AP,则△APQ面积最大值为( )
),点B(2,0),P为线段OB上一点,过点P作PQ∥OA,交AB于点Q,连接AP,则△APQ面积最大值为( ) 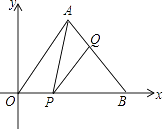
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com