
【题目】如图,⊙O的半径为 ![]() ,BD是⊙O的切线,D为切点,过圆上一点C作BD的垂线,垂足为B,BC=3,点A是优弧CD的中点,则sin∠A的值是( )
,BD是⊙O的切线,D为切点,过圆上一点C作BD的垂线,垂足为B,BC=3,点A是优弧CD的中点,则sin∠A的值是( ) 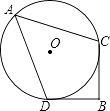
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解: 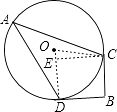
连接OC、OD,过C作CE⊥OD于E,
∵BD切⊙O于D,
∴BD⊥OD,
∵BC⊥BD,
∴∠B=∠BDE=∠CED=90°,
∴四边形CEDB是矩形,
∴BC=DE=3,
∵OD= ![]() ,
,
∴OE=OD﹣DE= ![]() ﹣3=
﹣3= ![]() ,
,
∴cos∠COE= ![]() =
= ![]() =
= ![]() ,
,
∵∠COD为弧CD对的圆心角,∠A为弧CD对的圆周角,
∴∠COD=2∠A,
∴cos2A= ![]() ,
,
∵1﹣2sin2A= ![]() ,
,
∴sinA= ![]() ,
,
故选C.
【考点精析】利用切线的性质定理对题目进行判断即可得到答案,需要熟知切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
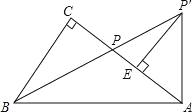
【题目】如图,在 Rt△ABC 中,∠C=90°,AP′⊥AB,BP′交 AC 于点 P, AP=AP′.
(1)求证:∠CBP=∠ABP;
(2)过点 P′作 P′E⊥AC 于点 E,求证:AE=CP.
查看答案和解析>>
科目:初中数学 来源: 题型:
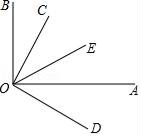
【题目】填空,完成下列说理过程
如图,∠AOB=90°,∠COD=90°,OA平分∠DOE,若∠BOC=20°,求∠COE的度数
解:因为∠AOB=90°.
所以∠BOC+∠AOC=90°
因为∠COD=90°
所以∠AOD+∠AOC=90°.
所以∠BOC=∠AOD. ( )
因为∠BOC=20°.
所以∠AOD=20°.
因为OA平分∠DOE
所以∠ =2∠AOD= °. ( )
所以∠COE=∠COD﹣∠DOE= °
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 已知A(-4,-1),B(-5,-4),C(-1,-3),△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)。
(1)请在图中作出△A′B′C′;(2)写出点A′、B′、C′的坐标.
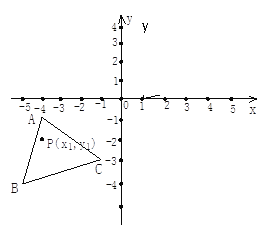
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将7张如图1所示的长为a,宽为b(a>b)的小长方形纸片按图2所示的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,求a,b满足的条件.
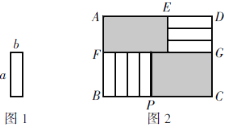
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠A=∠C,AD⊥BE于点F,BC⊥BE,点E,D,C在同一条直线上.
(1)判断AB与CD的位置关系,并说明理由;
(2)若∠ABC=120°,求∠BEC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题: 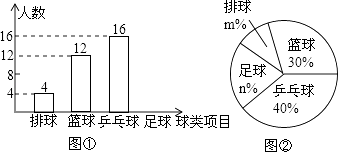
(1)九(1)班的学生人数为 , 并把条形统计图补充完整;
(2)扇形统计图中m= , n= , 表示“足球”的扇形的圆心角是度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七(1)班小明同学通过《测量硬币的厚度与质量》实验得到了每枚硬币的厚度和质量,数据如下表.他从储蓄罐取出一把5角和1元硬币,为了知道总的金额,他把这些硬币叠起来,用尺量出它们的总厚度为22.6mm,又用天平称出总质量为78.5g,请你帮助小明同学算出这把硬币的总金额为______元.
1元硬币 | 5角硬币 | |
每枚厚度(单位:mm) | 1.8 | 1.7 |
每枚质量(单位:g) | 6.1 | 6.0 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD;
(2)求证:AE⊥CD;
(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的有 (请写序号,少选、错选均不得分).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com