
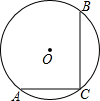
 如图,在⊙O中,弦AC⊥BC,若AC=6cm,BC=8cm,则⊙O的半径为5cm.
如图,在⊙O中,弦AC⊥BC,若AC=6cm,BC=8cm,则⊙O的半径为5cm. 分析 过点O作OE⊥AC,OF⊥BC,垂足分别为E、F,连接OC,故可得出OF=CE=$\frac{1}{2}$AC,CF=$\frac{1}{2}$BC,根据勾股定理即可得出结论.
解答 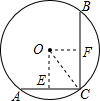 解:过点O作OE⊥AC,OF⊥BC,垂足分别为E、F,连接OC,
解:过点O作OE⊥AC,OF⊥BC,垂足分别为E、F,连接OC,
∵AC⊥BC,
∴∠ACB=∠OFC=∠OEC=90°,
∴四边形OEFC是矩形,
∴OF=CE=$\frac{1}{2}$AC=3cm,CF=$\frac{1}{2}$BC=4cm,
∴OC=$\sqrt{{OF}^{2}+{CF}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5cm.
故答案为:5.
点评 本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.


 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:解答题
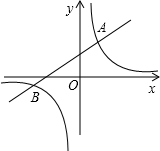 如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图象在第一象限相交于点A(1,-k+4)
如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图象在第一象限相交于点A(1,-k+4)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
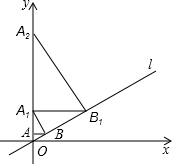 如图,已知直线l:y=$\frac{\sqrt{3}}{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂 线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为(0,42015)或(0,24030).
如图,已知直线l:y=$\frac{\sqrt{3}}{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂 线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为(0,42015)或(0,24030).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com