
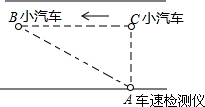
 规定:小汽车在城市街路上行驶速度不得超过60千米/小时,一辆小汽车在一条城市道路上自右向左行驶,某一时刻刚好行驶道路对面车速检测仪A的正前方C处,AC=30米.过了2秒后到达B处,测得小汽车与车速检测仪之间的距离AB为50米.这辆小汽车超速了吗?为什么?超速了多少?
规定:小汽车在城市街路上行驶速度不得超过60千米/小时,一辆小汽车在一条城市道路上自右向左行驶,某一时刻刚好行驶道路对面车速检测仪A的正前方C处,AC=30米.过了2秒后到达B处,测得小汽车与车速检测仪之间的距离AB为50米.这辆小汽车超速了吗?为什么?超速了多少?科目:初中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 3 |
| 3 |
| 2 |
| 1 |
| 3 |
| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
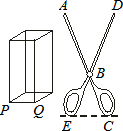 有一支夹子如图所示,AB=2BC,BD=2BE,在夹子前面有一个长方体硬物,厚PQ为6cm,如果想用夹子的尖端A、D两点夹住P、Q两点,那么手握的地方EC至少要张开
有一支夹子如图所示,AB=2BC,BD=2BE,在夹子前面有一个长方体硬物,厚PQ为6cm,如果想用夹子的尖端A、D两点夹住P、Q两点,那么手握的地方EC至少要张开查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com