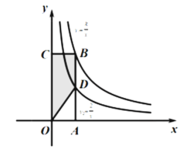
【题目】如图所示，在平面直角坐标系Oxy中，四边形OABC为矩形，点A、C分别在x轴、y轴上，点B在函数
（
，k为常数且
）的图象上，边AB与函数
的图象交于点D，则阴影部分ODBC的面积为________（结果用含k的式子表示）
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案科目：初中数学 来源： 题型：
【题目】如图，有四张正面标有数字
，背面颜色一样的卡片，正面朝下放在桌面上，小红从中随机抽取一张卡片记下数字，再从余下的卡片中随机抽取一张卡片记下数字．
(1)第一次抽到数字2的卡片的概率是 ；
(2)设第一次抽到的数字为
，第二次抽到的数字为
，点
的坐标为
，请用树状图或列表法求点在第三象限的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
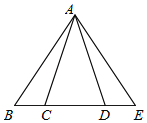
【题目】如图，在△ABE中，C，D是边BE上的两点，有下面四个关系式：（1）AB=AE，（2）BC=DE，（3）AC=AD，（4）∠BAC=∠EAD．请用其中两个作为已知条件，余下两个作为求证的结论，写出你的已知和求证，并证明．
已知：
求证：
证明：
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点A为⊙O外一点，连接AO，交⊙O于点P，AO=6．点B为⊙O上一点，连接BP，过点A作CA⊥AO，交BP延长线于点C，AC=AB．
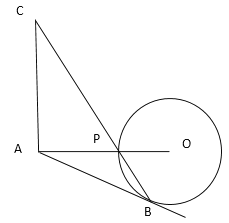
（1）判断直线AB与⊙O的位置关系，并说明理由．
（2）若PC=4
，求 PB的长．
（3）若在⊙O上存在点E，使△EAC是以AC为底的等腰三角形，则⊙O的半径r的取值范围是___________．
查看答案和解析>>
科目：初中数学 来源： 题型：
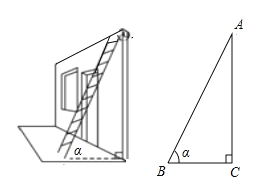
【题目】如图．要想使人安全地攀上斜靠在墙面上的梯子的顶端，梯子与地面所成的角
一般要满足
，现有一架长
的梯子．
（1）使用这架梯子最高可以安全攀上多高的墙（结果保留小数点后一位）？
（2）当梯子底端距离墙面
时，等于多少度（结果保留小数点后一位）？此时人是否能够安全使用这架梯子？
（参考数据：
，
，
，
，
，
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，
的顶点A在反比例函数
的图像上，直线AB交y轴于点C，且点C的纵坐标为5，过点A、B分别作y轴的垂线AE、BF，垂足分别为点E、F，且
．
（1）若点E为线段OC的中点，求k的值；
（2）若为等腰直角三角形，
，其面积小于3．
①求证：
；
②把
称为
，
两点间的“ZJ距离”，记为
，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了迎接“五一”小长假的购物高峰．某服装专卖店老板小王准备购进甲、乙两种夏季服装．其中甲种服装每件的成本价比乙种服装的成本价多20元，甲种服装每件的售价为240元比乙种服装的售价多80元．小王用4000元购进甲种服装的数量与用3200元购进乙种服装的数量相同．
（1）甲种服装每件的成本是多少元？
（2）要使购进的甲、乙两种服装共200件的总利润（利润=售价-进价）不少于21100元，且不超过21700元，问小王有几种进货方案？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】民间素有“肖县石榴砀山梨，汴梁西瓜红到皮”的谚语，汴梁西瓜是开封的传统特产，驰名古今，畅销中外，某批发商先购买了300千克黑皮无籽西瓜和200千克花皮无籽西瓜，共花费520元，几天后又购买了400千克黑皮无籽西瓜和300千克花皮无籽西瓜，共花费720元（每次两种西瓜的批发价不变），
（1）求黑皮无籽西瓜和花皮无籽西瓜的批发价分别是每千克多少元；
（2）该批发商一段时间后为满足市场需求，还需购买两种西瓜共800千克，要求黑皮无籽西瓜的数量不少于花皮西瓜的3倍，请设计一种购买方案，使所需总费用最低．
查看答案和解析>>
科目：初中数学 来源： 题型：
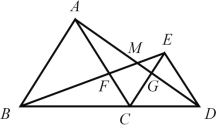
【题目】如图所示，
均为等边三角形，边长分别为
，B、C、D三点在同一条直线上，则下列结论正确的________________．（填序号）
①
②
③
为等边三角形 ④
⑤CM平分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
