
 已知:如图,PM=PN,∠M=∠N.求证:AM=BN.
已知:如图,PM=PN,∠M=∠N.求证:AM=BN.
分析 欲证明AM=AN,因为PM=PN,只要证明PA=PB即可,只要证明△PAN≌△PBM.
解答 证明:在△PAN和△PBM中,
$\left\{\begin{array}{l}{∠P=∠P(公共角)}\\{PN=PN(已知)}\\{∠N=∠M(已知)}\end{array}\right.$,
∴△PAN≌△PBM(ASA)
∴PA=PB(全等三角形对应边相等)
∵PM=PN(已知)
∴PM-PA=PN-PB,即AM=BN.
故答案分别为:PB,△PAN,△PBM,PAN.PBM,P,P,公共角,PM,PN,已知,N,M,已知,PAN,PBM,ASA,PB,全等三角形对应边相等,已知,PA,PB,BN.
点评 本题考查全等三角形的判定和性质、解题的关键是熟练掌握全等三角形判定方法,属于基础题,中考常考题型.


科目:初中数学 来源: 题型:解答题
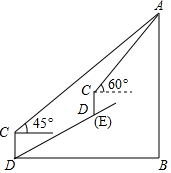 如图,在一次数学课外实践活动中,要求测量山坡前某建筑物的高度 AB.小刚在D处用高1.5m的测角仪CD,测得该建筑物顶端A的仰角为45°,然后沿倾斜角为30°的山坡向上前进20m到达E,重新安装好测角仪CD后又测得该建筑物顶端A的仰角为60°.求该建筑物的高度AB.(结果保留根号)
如图,在一次数学课外实践活动中,要求测量山坡前某建筑物的高度 AB.小刚在D处用高1.5m的测角仪CD,测得该建筑物顶端A的仰角为45°,然后沿倾斜角为30°的山坡向上前进20m到达E,重新安装好测角仪CD后又测得该建筑物顶端A的仰角为60°.求该建筑物的高度AB.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,有三条公路L1,L2,L3两两相交,若选择一地点建座加油站,使它到三条公路的距离都相等.应如何选择加油站的地址?这样的地址有几处?
如图所示,有三条公路L1,L2,L3两两相交,若选择一地点建座加油站,使它到三条公路的距离都相等.应如何选择加油站的地址?这样的地址有几处?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,数轴上A、B两点对应的数分别为6和10,点P从原点O出发,以每秒3个单位长度的速度沿数轴正方向运动,同时点Q从点A出发,以每秒1个单位长度的速度沿数轴正方向运动.设运动时间为t秒.
如图,数轴上A、B两点对应的数分别为6和10,点P从原点O出发,以每秒3个单位长度的速度沿数轴正方向运动,同时点Q从点A出发,以每秒1个单位长度的速度沿数轴正方向运动.设运动时间为t秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com