Question

17．如图，花边上正三角形的内切圆半径1cm，如果这条花边中有100个圆和100个正三角形，算一算这条花边的总长度．

Answer 1

分析 画出图形，连接AD，OB，则AD过O，求出∠OBD=30°，求出OB，根据勾股定理求出BD，同法求出CD，求出BC的长后求得花边的周长．

解答 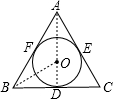解：从中选择一个等边三角形和其内接圆如图，⊙O是△ABC的内切圆，⊙O切AB于F，切AC于E，切BC于D，
连接AD，OB，则AD过O（因为等边三角形的内切圆的圆心再角平分线上，也在底边的垂直平分线上），
∵△ABC是等边三角形，
∴∠ABC=60°，
∵⊙O是△ABC的内切圆，
∴∠OBC=$\frac{1}{2}$∠ABC=30°，
∵⊙O切BC于D，
∴∠ODB=90°，
∵OD=1cm，
∴OB=2cm，
由勾股定理得：BD=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$（cm），
∴BC=2$\sqrt{3}$（cm），
∴这条花边的总长度为：2$\sqrt{3}$+2$\sqrt{3}$+200×2$\sqrt{3}$=404$\sqrt{3}$（cm）．

点评 本题考查了三角形的内切圆与圆心的知识，解题的关键是计算一个等边三角形的边长，难度中等．