练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    数学活动课上，老师在黑板上画直线l平行于射线AN（如图），让同学们在直线L和射线AN上各找一点B和C，使得以A、B、C为顶点的三角形是等腰直角三角形．这样的三角形最多能画（　　）
    A、1个B、2个C、3个D、4个
    考点：等腰直角三角形
    专题：
    分析：以A为一个顶点，射线和直线之间的距离为边长作正方形，可得到两个等腰直角三角形，再以这个正方形的对角线为腰又可得到一个，可得到答案．
    解答：解：如图，以A为一个顶点，射线和直线之间的距离为边长作正方形ABCD，
    连接AC，BD，
    根据正方形的性质可知△ABC和△ADC都是等腰直角三角形，
    再以AC为腰，可作直角三角形ACE，
    所以满足条件的三角形有三个，
    故选C．
    点评：本题主要考查等腰直角三角形的判定，根据题意判断出直角三角形的位置是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    若
    2
    x
    =
    3
    y
    =
    5
    z
    ，且3x+2y-z=14，求x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

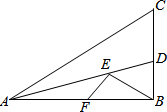    如图，在Rt△ABC中，AC=6，AB=3
    		3
    ，∠BAC=30°，∠BAC的平分线交BC于点D，E、F分别是线段AD和AB上的动点，求BE+EF的最小值
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

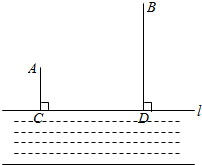    如图，已知A，B两个村庄在河流CD的同侧，它们到河流的距离AC=10km，BD=30km，且CD=30km．现在要在河流CD上建立一个泵站P向村庄供水，铺设管道的费用为每千米2万元，要使所花费用最少，请确定泵站P的位置？（保留痕迹，不写作法）此时所花费用最少为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    当时钟3时25分时，时针与分针的夹角的度数是多少﹖

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，线段AB上两点C、D，AB=30cm，AC=10cm，BD=5cm，点P从A出发以每秒1cm的速度，沿A→C→D→B→D运动，点Q从B出发，沿B→D→C→A→C运动，P，Q两点运动到终点D，C后停止运动，当Q到达D点时，PA=
    1
    3
    PC，设点P运动时间为t s．
    （1）求点Q的运动速度；
    （2）是否存在某一时间，使PQ=18cm？若存在，求出t的值，若不从在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    36.3°-16°20″=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

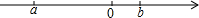    实数a、b在数轴上的位置如图所示，给出如下结论：①a+b＞0；②b-a＞0；③-a＞b；④a＞-b，⑤|a|＞|b|＞0．其中正确的结论是（　　）
    A、①②③B、②③④
    C、②③⑤D、②④⑤

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    解方程：x-
    2x-1
    3
    =
    x+3
    2
    ．

    查看答案和解析>>

    同步练习册答案