
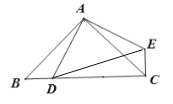
【题目】如图,在△ABC中,∠BAC=90°,AC=AB,点D为BC边上的一个动点(点D不与B,C重合),以AD为边作等腰直角△ADE,∠DAE=90°,连接CE.
(1)求证:△ABD≌△ACE.
(2)试猜想线段BD,CD,DE之间的等量关系,并证明你的猜想.
科目:初中数学 来源: 题型:
【题目】如图,D,E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( ) 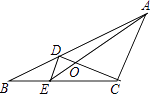
A.1:3
B.1:4
C.1:5
D.1:25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y= ![]() 的图象经过点(2,3),那么下列四个点中,也在这个函数图象上的是( )
的图象经过点(2,3),那么下列四个点中,也在这个函数图象上的是( )
A.(﹣6,1)
B.(1,6)
C.(2,﹣3)
D.(3,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学在一次用频率去估计概率的实验中,统计了某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( )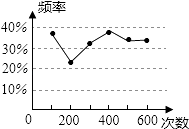
A.掷一枚正六面体的骰子,出现1点的概率
B.从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率
C.抛一枚硬币,出现正面的概率
D.任意写一个整数,它能被2整除的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某超市地下停车场入口的设计图,请根据图中数据计算CE的长度.(结果保留小数点后两位;参考数据:sin22°=0.3746,cos22°=0.9272,tan22°=0.4040)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温度与我们的生活息息相关,如图是一个温度计实物示意图,左边的刻度是摄氏温度(℃),右边的刻度是华氏温度(℉).设摄氏温度为x(℃)华氏温度为y(℉),则y是x的一次函数,通过观察我们发现,温度计上的摄氏温度为0℃时,华氏温度为32℉;摄氏温度为﹣20℃时,华氏温度为﹣4℉

请根据以上信息,解答下列问题
(1)仔细观察图中数据,试求出y与x的函数关系式;
(2)当摄氏温度为﹣5℃时,华氏温度为多少?
(3)当华氏温度为59℉时,摄氏温度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于函数y= ![]() ,下列说法错误的是( )
,下列说法错误的是( )
A.这个函数的图象位于第一、第三象限
B.当x>0时,y随x的增大而增大
C.这个函数的图象既是轴对称图形又是中心对称图形
D.当x<0时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,D在AB同侧,∠CAB=∠DBA,下列条件中不能判定△ABD≌△BAC的是( )

A. ∠D=∠C B. BD=AC C. ∠CAD=∠DBC D. AD=BC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com