
【题目】如图,已知一次函数y= ![]() x-3与反比例函数y=
x-3与反比例函数y= ![]() 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.
(1)填空:n的值为 , k的值为;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比函数y= ![]() 的图象,当y≥-2时,请直接写出自变量x的取值范围.
的图象,当y≥-2时,请直接写出自变量x的取值范围.
【答案】
(1)3,12
(2)解:∵一次函数y= ![]() x-3与x轴相交于点B,
x-3与x轴相交于点B,
∴ ![]() x-3=0,
x-3=0,
解得x=2,
∴点B的坐标为(2,0),
如图,过点A作AE⊥x轴,垂足为E,过点D作DF⊥x轴,垂足为F,
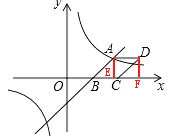
∵A(4,3),B(2,0),
∴OE=4,AE=3,OB=2,
∴BE=OE-OB=4-2=2,
在Rt△ABE中,
AB= ![]() ,
,
∵四边形ABCD是菱形,
∴AB=CD=BC= ![]() ,AB∥CD,
,AB∥CD,
∴∠ABE=∠DCF,
∵AE⊥x轴,DF⊥x轴,
∴∠AEB=∠DFC=90°,
在△ABE与△DCF中,
 ,
,
∴△ABE≌△DCF(ASA),
∴CF=BE=2,DF=AE=3,
∴OF=OB+BC+CF=2+ ![]() +2=4+
+2=4+ ![]() ,
,
∴点D的坐标为(4+ ![]() ,3)
,3)
(3)解:当y=-2时,-2= ![]() ,解得x=-6.
,解得x=-6.
故当y≥-2时,自变量x的取值范围是x≤-6或x>0
【解析】解:(1)把点A(4,n)代入一次函数y= ![]() x-3,可得n=
x-3,可得n= ![]() ×4-3=3;
×4-3=3;
把点A(4,3)代入反比例函数 ![]() ,可得3=
,可得3= ![]() ,
,
解得k=12.
(1)把点A(4,n)代入一次函数,求出n的值,把点A(4,3)代入反比例函数 ,求出k的值;(2)由一次函数与x轴相交于点B,求出点B的坐标,根据已知和勾股定理求出AB的值,由四边形ABCD是菱形,根据菱形的性质,得到△ABE≌△DCF,根据全等三角形的对应边相等,求出DF=AE和OF的值,得到点D的坐标;(3)当y=-2时,求出x的值,得到自变量x的取值范围.


科目:初中数学 来源: 题型:
【题目】操作探究:已知在纸面上有一数轴(如图所示),
![]()
(1)折叠纸面,使表示的点1与-1重合,则-2表示的点与 表示的点重合;
(2)折叠纸面,使-1表示的点与3表示的点重合,回答以下问题:
① 5表示的点与数 表示的点重合;
②![]() 表示的点与数 表示的点重合;
表示的点与数 表示的点重合;
③若数轴上A、B两点之间距离为9(A在B的左侧),且A、B两点经折叠后重合,此时点A表示的数是 、点B表示的数是 .
(3)已知在数轴上点A表示的数是a,点A移动4个单位,此时点A表示的数和a是互为相反数,求a的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,﹣1),B(﹣5,﹣4),C(﹣1,﹣3),△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).
(1)请在图中作出△A′B′C′;
(2)写出点A′、B′、C′的坐标;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(﹣1,5),B(﹣4,1),C(﹣1,1)将△ABC绕点A逆时针旋转90°,得到△AB′C′,点B,C的对应点分别为点B′,C′,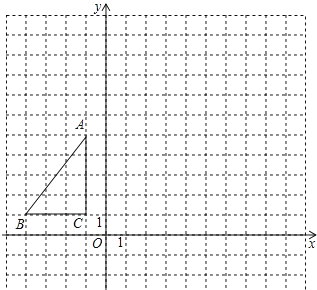
(1)画出△AB′C′;
(2)写出点B′,C′的坐标;
(3)求出在△ABC旋转的过程中,点C经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙二人驾车分别从A,B两地同时出发,相向而行.下图是二人离A地的距离y(千米)与所用时间x(小时)的关系.
(1)请说明交点P所表示的实际意义: ;
(2)试求出A,B两地之间的距离;
(3)甲从A地到达B地所需的时间为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列证明过程,并在括号中填上理论依据.
如图,已知AC⊥AE垂足为A,BD⊥BF垂足为B,∠1=35°,∠2=35°.

证明:AC∥BD; AE∥BF.
证明:∵∠1=∠2=35°,
∴ ∥ ( )
∵AC⊥AE,BD⊥BF,
∴∠ =∠ =90°
又∵∠1=∠2=35°,
∴∠ =∠
∴EA∥BF( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中, BD是∠ABC的平分线,过点C作CE⊥BD,交 BD的延长线于点E,∠ABC=60°,∠ECD=15°.
(1)直接写出∠ADB的度数是_______;
(2)求证:BD=AB;
(3)若AB=2,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知边长为m的正方形面积为12,则下列关于m的说法中,错误的是( )
①m是无理数;②m是方程m2 -12=0的解;③m满足不等式组![]() ,④m是12的算术平方根.
,④m是12的算术平方根.
A. ①② B. ①③ C. ③ D. ①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com