
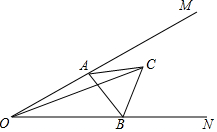
 如图,∠MON=30°,点A、B分别为OM、ON上的点,AB=2,以AB为边作等边三角形ABC,则OC的最大值为2+2$\sqrt{3}$.(参考数据:tan75°=2+$\sqrt{3}$)
如图,∠MON=30°,点A、B分别为OM、ON上的点,AB=2,以AB为边作等边三角形ABC,则OC的最大值为2+2$\sqrt{3}$.(参考数据:tan75°=2+$\sqrt{3}$) 分析 当AB垂直∠MON的平分线时,OC最大,设AB交OC于D,根据等边三角形的性质得到AD=1,根据三角形的内角和得到∠OAH=75°,解直角三角形即可得到结论.
解答  解:取AB的中点D,连接OD,CD,当O,C,D三点共线时,
解:取AB的中点D,连接OD,CD,当O,C,D三点共线时,
OC有最大值,∵AB=2,△ABC是等边三角形,
∴AD=BD=1,
∵OC是∠MON的平分线,
∴∠MOC=15°,
∴∠OAD=75°,
∵tan∠OAD=tan75°=$\frac{OD}{BD}$=2+$\sqrt{3}$,
∴OD=2+$\sqrt{3}$,DC=$\sqrt{3}$,
∴OC=OD+CD=2+2$\sqrt{3}$.
故答案为:2+2$\sqrt{3}$.
点评 本题考查了等边三角形的性质,解直角三角形,知道当AB垂直∠MON的平分线时,OC最大是解题的关键.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}{x^2}$-x=9 | B. | x3-x2+40=0 | C. | $\frac{4}{x-1}$=3 | D. | 3x3-2xy+y2=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 将正整数按如图所示的规律排列下去,若有序实数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示实数9.寻找规律,然后解答:
将正整数按如图所示的规律排列下去,若有序实数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示实数9.寻找规律,然后解答:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com