
分析 (1)、(2)、(3)先根据二次根式有意义的条件求出x的取值范围即可;
(4)根据二次根式及分式有意义的条件列出关于x的不等式组,求出x的取值范围即可.
解答 解:(1)∵$\sqrt{x-4}$有意义,
∴x-4≥0,即x≥4;
(2)∵$\sqrt{1+{x}^{2}}$有意义,
∴1+x2≥0,
∴x为全体实数;
(3)∵$\sqrt{4-6x}$有意义,
∴4-6x≥0,解得x≤$\frac{2}{3}$;
(4)∵$\frac{1}{\sqrt{2-3x}}$有意义,
∴$\left\{\begin{array}{l}2-3x≥0\\ 2-3x≠0\end{array}\right.$,解得x<$\frac{2}{3}$.
点评 本题考查的是二次根式有意义的条件,熟知二次根式具有非负性是解答此题的关键.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
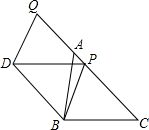 如图,在△ABC中,AB=8,sin∠BAC=$\frac{3}{4}$,点P为AC边上任意一点,点Q为CA延长线上任意一点,以PB、PQ为两边作?PQDB,则对角线PD的最小值为6.
如图,在△ABC中,AB=8,sin∠BAC=$\frac{3}{4}$,点P为AC边上任意一点,点Q为CA延长线上任意一点,以PB、PQ为两边作?PQDB,则对角线PD的最小值为6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com