
分析 (1)先提取公因式x,再对余下的多项式利用平方差公式继续分解;
(2)先提取公因式2,再对余下的多项式利用平方差公式继续分解;
(3)利用平方差公式分解因式,再整理即可得解;
(4)先提取公因式5x,再对余下的多项式利用平方差公式继续分解.
解答 解:(1)x3-xy2,
=x(x2-y2),
=x(x+y)(x-y);
(2)2x2-8,
=2(x2-4),
=2(x+2)(x-2);
(3)36(x+2y)2-25(x-2y)2,
=[6(x+2y)+5(x-2y)][6(x+2y)-5(x-2y)],
=(11x+2y)(x+22y);
(4)5x3-20xy2,
=5x(x2-4y2),
=5x(x+2y)(x-2y).
故答案为:(1)x(x+y)(x-y);(2)2(x+2)(x-2);(3)(11x+2y)(x+22y);(4)5x(x+2y)(x-2y).
点评 本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
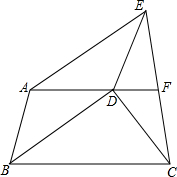 A、D、F在同一直线上,F是CE的中点,EC⊥BC、BA∥DE,BD∥AE.甲、乙两人同时从住所B地步行到F地办公,若甲走的路线是B-A-E-F;乙走的路线是B-D-C-F,假设两人行走的速度相同,那么谁先到达办公地点F?请说明理由.
A、D、F在同一直线上,F是CE的中点,EC⊥BC、BA∥DE,BD∥AE.甲、乙两人同时从住所B地步行到F地办公,若甲走的路线是B-A-E-F;乙走的路线是B-D-C-F,假设两人行走的速度相同,那么谁先到达办公地点F?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=$\sqrt{x-1}(x≥1)$ | B. | y=-$\sqrt{x-1}(x≥1)$ | C. | y=$\sqrt{1-x}(x≤1)$ | D. | y=±$\sqrt{1-x}(x≤1)$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
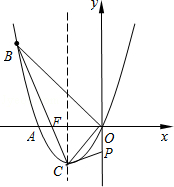 如图,已知抛物线经过A(-2,0),B(-3,3)及原点O,顶点为C.
如图,已知抛物线经过A(-2,0),B(-3,3)及原点O,顶点为C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
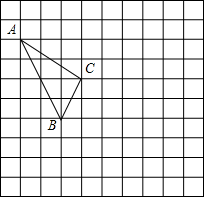 已知△ABC的顶点A(-4,5),B(-2,1),完成下列问题:
已知△ABC的顶点A(-4,5),B(-2,1),完成下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com