
【题目】如图,在△ABC中,AB = AC,点D是边BC的中点,过点A、D分别作BC与AB的平行线,相交于点E,连结EC、AD.
求证:四边形ADCE是矩形.

【答案】证明见解析
【解析】试题分析:先由AB=AC,点D是边BC的中点,根据等腰三角形三线合一的性质得出BD=CD,AD⊥BC,再由AE∥BD,DE∥AB,得出四边形AEDB为平行四边形,那么AE=BD=CD,又AE∥DC,根据一组对边平行且相等的四边形是平行四边形得出四边形ADCE是平行四边形,又∠ADC=90°,根据有一个角是直角的平行四边形即可证明四边形ADCE是矩形;
试题解析:∵AB=AC,点D是边BC的中点,
∴BD=CD,AD⊥BC,
∴∠ADC=90°.
∵AE∥BD,DE∥AB,
∴四边形AEDB为平行四边形,
∴AE=BD=CD,
又∵AE∥DC,
∴四边形ADCE是平行四边形,
∵∠ADC=90°,
∴四边形ADCE是矩形.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】工人师傅用![]() 米长的铝合金材料制作一个如图所示的矩形窗框,图中的①、②、③区域都是矩形,且
米长的铝合金材料制作一个如图所示的矩形窗框,图中的①、②、③区域都是矩形,且![]() ,
,![]() ,
,![]() 分别是
分别是![]() 、
、![]() 的中点.(说明:图中黑线部分均需要使用铝合金材料制作,铝合金材料宽度忽略不计).
的中点.(说明:图中黑线部分均需要使用铝合金材料制作,铝合金材料宽度忽略不计).

![]() 当矩形窗框
当矩形窗框![]() 的透光面积是
的透光面积是![]() 平方米时,求
平方米时,求![]() 的长度.
的长度.
![]() 当
当![]() 为多长时,矩形窗框
为多长时,矩形窗框![]() 的透光面积最大?最大面积是多少?
的透光面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:如图1,在![]() 中,D、E分别是AB、AC两边的中点,延长DE至点F,使
中,D、E分别是AB、AC两边的中点,延长DE至点F,使![]() ,连结
,连结![]() 易知
易知![]() ≌
≌![]() .
.



探究:如图2,AD是![]() 的中线,BE交AC于点E,交AD于点F,且
的中线,BE交AC于点E,交AD于点F,且![]() ,求证:
,求证:![]() .
.
应用:如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,DE是
,DE是![]() 的中位线
的中位线![]() 过点D、E作
过点D、E作![]() ,分别交边BC于点F、G,过点A作
,分别交边BC于点F、G,过点A作![]() ,分别与FD、GE的延长线交于点M、N,则四边形MFGN周长C的取值范围是______.
,分别与FD、GE的延长线交于点M、N,则四边形MFGN周长C的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,它们的形状、大小、质地等完全相同.小强先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
(1)用列表法或画树状图表示出(x,y)的所有可能出现的结果;
(2)求小强、小华各取一次小球所确定的点(x,y)落在一次函数![]() 图象上的概率;
图象上的概率;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F,

(1)求∠F的度数;
(2)若CD=5,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂安排甲、乙两个运输队各从仓库调运物资300吨,两队同时开始工作,甲运输队工作3天后因故停止,2天后重新开始工作,由于工厂调离了部分工人,甲运输的工作效率降低到原来的![]() 甲、乙运输队调运物资的数量
甲、乙运输队调运物资的数量![]() 吨
吨![]() 与甲工作时间
与甲工作时间![]() 天
天![]() 的函数图象如图所示.
的函数图象如图所示.
![]() ______;
______;![]() ______.
______.
![]() 求甲运输队重新开始工作后,甲运输队调运物资的数量
求甲运输队重新开始工作后,甲运输队调运物资的数量![]() 吨
吨![]() 与工作时间
与工作时间![]() 天
天![]() 的函数关系式;
的函数关系式;
![]() 直接写出乙运输队比甲运输队多运50吨物资时x的值.
直接写出乙运输队比甲运输队多运50吨物资时x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一渔船在海岛![]() 南偏东
南偏东![]() 方向的
方向的![]() 处遇险,测得海岛
处遇险,测得海岛![]() 与
与![]() 的距离为
的距离为![]() 海里,渔船将险情报告给位于
海里,渔船将险情报告给位于![]() 处的救援船后,沿北偏西
处的救援船后,沿北偏西![]() 方向向海岛
方向向海岛![]() 靠近,同时,从
靠近,同时,从![]() 处出发的救援船沿南偏西
处出发的救援船沿南偏西![]() 方向匀速航行,
方向匀速航行,![]() 分钟后,救援船在海岛
分钟后,救援船在海岛![]() 处恰好追上渔船,那么救援船航行的速度为( )
处恰好追上渔船,那么救援船航行的速度为( )

A. 10![]() 海里/小时 B. 30海里/小时 C. 20
海里/小时 B. 30海里/小时 C. 20![]() 海里/小时 D. 30
海里/小时 D. 30![]() 海里/小时
海里/小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两店分另选5名销售员某月的销售额(单位:万元)进行分析,数据如下图表(不完整):
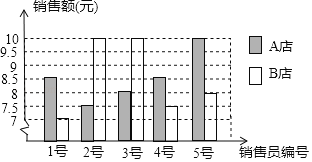
平均数 | 中位数 | 众数 | |
A店 | 8.5 |
|
|
B店 |
| 8 | 10 |
(1)根据图a数据填充表格b所缺的数据;
(2)如果A店想让一半以上的销售员达到销售目标,你认为月销售额定为多少合适?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com