
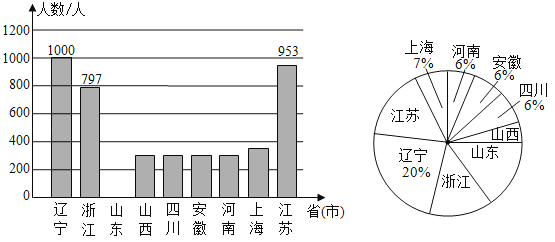
【题目】2020年春节前夕“新型冠状病毒”爆发,疫情就是命令,防控就是使命.全国各地驰援武汉的医护工作者,践行医者仁心的使命与担当,舍小家,为大家,用自己的专业知识与血肉之躯构筑起全社会抗击疫情的钢铁长城.下面是2月9日当天全国部分省市驰援武汉医护工作者的人数统计图(不完整).
请解答下列问题:
(1)①上述省市2月9日当天驰援武汉的医护工作者的总人数为 人;
②请将条形统计图补充完整;
(2)请求出扇形统计图中“山东”所对应扇形的圆心角的度数;
(3)本次山东驰援武汉的医护工作者中,有5人报名去重症区,王医生和李医生就在其中,若从报名的5人中随机安排2人,求同时安排王医生和李医生的概率.
【答案】(1)①5000;②见解析;(2)72°;(3)![]()
【解析】
(1)①用辽宁驰援武汉的医护工作者的人数除以它所占的百分比得到调查的总人数;
②先计算出山东援武汉的医护工作者的人数,然后补全图形统计图;
(2)用山东援武汉的医护工作者的人数所占的百分比乘以360°得到扇形统计图中“山东”所对应扇形的圆心角的度数;
(3)画树状图(用A、D表示王医生和李医生)展示所有20种等可能的结果数,再找出同时安排王医生和李医生的结果数,然后根据概率公式求解.
(1)①1000÷20%=5000,
所以上述省市2月9日当天驰援武汉的医护工作者的总人数为5000人;
故答案为5000;
②山东援武汉的医护工作者的人数为5000﹣1000﹣797﹣953﹣5000(7%+6%+6%+6%)=1000(人),
条形统计图补充为:
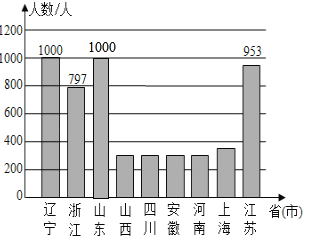
(2)扇形统计图中“山东”所对应扇形的圆心角的度数=360°×![]() =72°;
=72°;
(3)画树状图为:(用A、D表示王医生和李医生)
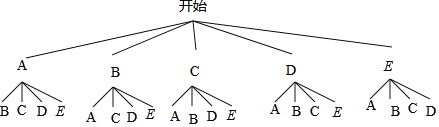
共有20种等可能的结果数,其中同时安排王医生和李医生的结果数为2,
所以同时安排王医生和李医生的概率=![]() =
=![]() .
.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
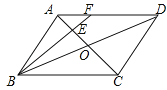
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
A. ①②③④ B. ①④ C. ②③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
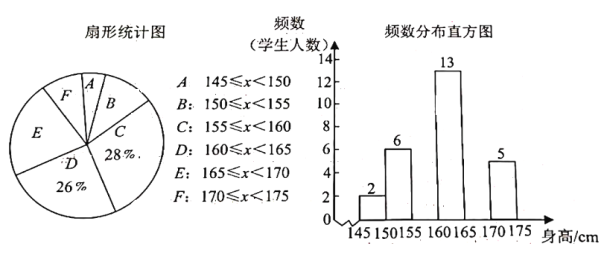
【题目】体育老师统计了七年级甲、乙两个班女生的身高情况,并绘制了如下不完整的统计图.请根据图中信息,解决下列问题:
(1)求甲、乙两个班共有女生多少人?
(2)请将频数分布直方图补充完整;
(3)求扇形统计图中![]() 部分所对应的扇形圆心角的度数.
部分所对应的扇形圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】书法是我国的文化瑰宝,研习书法能培养高雅的品格.某校为加强书法教学,了解学生现有的书写能力,随机抽取了部分学生进行测试,测试结果分为优秀、良好、及格、不及格四个等级,分别用A,B,C,D表示,并将测试结果绘制成如图两幅不完整的统计图.
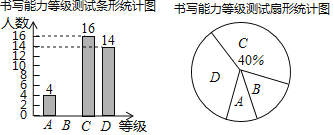
请根据统计图中的信息解答以下问题:
(1)本次抽取的学生人数是 ,扇形统计图中A所对应扇形圆心角的度数是 .
(2)把条形统计图补充完整.
(3)若该学校共有2800人,等级达到优秀的人数大约有多少?
(4)A等级的4名学生中有3名女生1名男生,现在需要从这4人中随机抽取2人参加电视台举办的“中学生书法比赛”,请用列表或画树状图的方法,求被抽取的2人恰好是1名男生1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( )
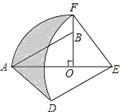
A. π B. ![]() C. 3+π D. 8﹣π
C. 3+π D. 8﹣π
查看答案和解析>>
科目:初中数学 来源: 题型:
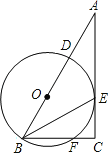
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
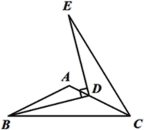
【题目】如图,在△ABC中,AB=AC=10,BC=![]() ,D为边AC上一动点(C点除外),把线段BD绕着点D沿着顺时针的方向旋转90°至DE,连接CE,则△CDE面积的最大值为______.
,D为边AC上一动点(C点除外),把线段BD绕着点D沿着顺时针的方向旋转90°至DE,连接CE,则△CDE面积的最大值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个四边形的对角线把四边形分成两个三角形,一个是等边三角形,另一个是该对角线所对的角为60°的三角形,我们把这条对角线叫做这个四边形的理想对角线,这个四边形称为理想四边形.
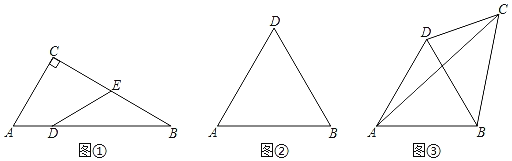
(1)如图①,在Rt△ABC中∠C=90°,∠B=30°,AC=4,D为AB上一点,AD=2,E为BC中点,连接DE.求证:四边形ADEC为理想四边形;
(2)如图②,△ABC是等边三角形,若BD为理想对角线,四边形ABCD为理想四边形.请画图找出符合条件的C点落在怎样的图形上;
(3)在(2)的条件下,
①若△BCD为直角三角形,BC=3,求AC的长度;
②如图③,若CD=x,BC=y,AC=z,请直接写出x,y,z之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com