练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．任意写出一个偶数和一个奇数，两数之和是奇数的概率是1，两数之和是偶数的概率是0．

    分析 利用不可能事件的概率为0，必然事件的概率为1求解．

    解答 解：一个奇数与一个偶数的和为奇数，
    所以任意写出一个偶数和一个奇数，两数之和是奇数的概率是1，两数之和是偶数的概率为0．
    故答案为1，0．

    点评 本题考查了列表法或树状图法：通过列表法或树状图法展示所有等可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求出事件A或B的概率．也考查了确定事件的概率．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．计算：
    （1）（$\sqrt{18}$-4$\sqrt{\frac{1}{2}}$+$\frac{1}{\sqrt{2}-\sqrt{3}}$）÷$\frac{\sqrt{3}}{3}$       
    （2）解不等式组：$\left\{\begin{array}{l}{x-1＞2}&{①}\\{x-3≤2+\frac{1}{2}x}&{②}\end{array}\right.$
    （3）$\left\{\begin{array}{l}{\frac{2x+1}{5}+\frac{3y-2}{4}=2}\\{\frac{3x-1}{5}-\frac{3y+2}{4}=0}\end{array}\right.$                   
    （4）$\left\{\begin{array}{l}{x+3y-z=8}\\{5x+3y+3z=20}\\{x-6y+z=1}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．阅读材料：如果是一元二次方程ax2+bx+c=0（a≠0）的两根，那么x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$，这就是著名的韦达定理．现在我们利用韦达定理解决问题：
    已知m与n是方程2x2-6x+3=0的两根
    （1）填空：m+n=3，m•n=$\frac{3}{2}$；
    （2）计算$\frac{1}{m}+\frac{1}{n}$与m2+n2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．先仔细阅读材料，再尝试解决问题：
    完全平方公式x2±2xy+y2=（x±y）2及（x±y）2的值恒为非负数的特点在数学学习中有着广泛的应用，比如探求多项式2x2+12x-4的最大（小）值时，我们可以这样处理：
    解：原式=2（x2+6x-2）
    =2（x2+6x+9-9-2）
    =2[（x+3）2-11]
    =2（x+3）2-22
    因为无论x取什么数，都有（x+3）2的值为非负数，所以（x+3）2的最小值为0，此时x=-3，进而2（x+3）2-22的最小值是2×0-22=-22，所以当x=-3时，原多项式的最小值是-22
    解决问题：
    请根据上面的解题思路，探求
    （1）多项式3x2-6x+12的最小值是多少，并写出对应的x的取值．
    （2）多项式-x2-2x+8的最大值是多少，并写出对应的x的取值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．如图，平面内有公共端点的六条射线OA，OB，OC，OD，OE，OF，从射线OA开始按逆时针方向依次在射线上写出数字1、2、3、4、5、6、7…，则数字
    “2016”在射线OF上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．己知：x=3是方程$\frac{x}{3}$+$\frac{m（x-1）}{4}$=2的解，n满足关系式|2n+m丨=1，求m+n的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．计算
    （1）2×（-3）-（-6）+1
    （2）（-2）2-|-7|+3÷（-1）3-2×（-$\frac{1}{2}$）
    （3）x-2=7x+1
    （4）$\frac{y-1}{2}$=2-$\frac{y+2}{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．已知M=2x2-5xy+6y2，N=3y2-4xy+2x2，求M-2N，并求当x=-1，y=2时，M-2N的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

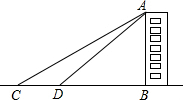    10．某中学九年级学生开展测量物体高度的实践活动，他们要测量学校一幢教学楼的高度，如图，他们先在点C测得教学楼AB的顶点A的仰角为30°，然后向教学楼前进20米到达点D，又测得点A的仰角为45°，请根据这些数据，求这幢教学楼的高度．（最后结果精确到1米，参考数据$\sqrt{2}≈1.414，\sqrt{3}$≈1.732）

    查看答案和解析>>

    同步练习册答案