
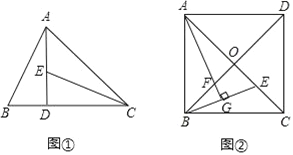
【题目】【阅读发现】如图①,在△ABC中,∠ACB=45°,AD⊥BC于点D,E为AD上一点,且DE=BD,可知AB=CE.
【类比探究】如图②,在正方形ABCD中,对角线AC与BD交于点O,E是OC上任意一点,AG⊥BE于点G,交BD于点F.判断AF与BE的数量关系,并加以证明.
【推广应用】在图②中,若AB=4,BF=![]() ,则△AGE的面积为 .
,则△AGE的面积为 .
【答案】【阅读发现】理由见解析;【类比探究】AF=BE,理由见解析;【推广应用】![]() .
.
【解析】试题分析:【阅读发现】证明△ACD是等腰直角三角形,得出AD=CD,由SAS证明△ABD≌△CED,即可得出AB=CE;
【类比探究】由AAS证明△ABF≌△BCE,即可得出AF=BE;
【推广应用】由勾股定理求出BD=![]() =4
=4![]() ,得出OA=OB=OC=
,得出OA=OB=OC=![]() BD=2
BD=2![]() ,求出OF=OB﹣BF=
,求出OF=OB﹣BF=![]() ,由勾股定理得出AF=
,由勾股定理得出AF=![]() =
=![]() ,由ASA证明△OBE≌△OAF,得出OE=OE=
,由ASA证明△OBE≌△OAF,得出OE=OE=![]() ,求出AE=OA+OE=3
,求出AE=OA+OE=3![]() ,证明△AOF∽△AGE,得出对应边成比例求出GE=
,证明△AOF∽△AGE,得出对应边成比例求出GE=![]() ,AG=
,AG=![]() ,即可得出△AGE的面积.
,即可得出△AGE的面积.
试题解析:【阅读发现】∵AD⊥BC,∠ACB=45°,
∴∠ADB=∠CDE=90°,△ACD是等腰直角三角形,
∴AD=CD,
在△ABD和△CED中, 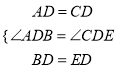 ,
,
∴△ABD≌△CED(SAS),
∴AB=CE;
【类比探究】AF=BE;理由如下:
∵正方形ABCD中,AB=BC=AD,∠BAD=90°,∠ABF=∠BCE=45°,AC⊥BD,OA=OB=OC,
∵AG⊥BE,
∴∠FAD+∠AFO=90°,
∵AG⊥BE,
∴∠FAO+∠AEG=90°,
∴∠AFO=∠AEG,
∵∠AFB=∠FAO+90°,
∴∠AFB=∠BEC,
在△ABF和△BCE中, 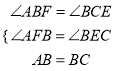 ,
,
∴△ABF≌△BCE(AAS),
∴AF=BE;
【推广应用】∵AB=AD=4,∠BAD=90°,
∴BD=![]() =4
=4![]() ,
,
∴OA=OB=OC=![]() BD=2
BD=2![]() ,
,
∵BF=![]() ,
,
∴OF=OB﹣BF=![]() ,
,
∴AF=![]() =
=![]() ,
,
由角的互余性质得:∠OAF=∠OBE,
在△OBE和△OAF中, 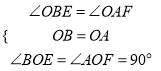 ,
,
∴△OBE≌△OAF(ASA),
∴OE=OE=![]() ,
,
∴AE=OA+OE=3![]() ,
,
∵∠OAF=∠GAE,∠AOF=∠AGE=90°,
∴△AOF∽△AGE,
∴![]() ,即
,即![]() ,
,
解得:GE=![]() ,AG=
,AG=![]() ,
,
∴△AGE的面积=![]() AGGE=
AGGE=![]() ×
×![]() ×
×![]() =
=![]() ;
;
故答案为: ![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,⊙O是△ABC的外接圆,AP是⊙O的切线.已知AC=4,BC=5.

(1)求证:∠PAC=∠ABC;
(2)作∠BAC的平分线,与⊙O相交于点D,与BC相交于点E,连接并延长DC,与AP相交于点F(如图2),若AE=AC,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,为了解市民对售后评价的关注情况,随机采访部分市民,对采访情况制作了如下统计图表:
关注情况 | 频数 | 频率 |
A.高度关注 | 50 | b |
B.一般关注 | 120 | 0.6 |
C.不关注 | a | 0.1 |
D.不知道 | 10 | 0.05 |
(1)根据上述统计图可得此次采访的人数为 人,a= ,b= ;
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,请估计在6400名市民中,高度关注售后评价的市民约有多少人?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com