
����Ŀ��Ϊ�˽������У����ѧ���п��������Գɼ����ֶԽ�����У�����п��������Գɼ����г������飬���ͳ�����£���������ͳ��ͼ��C�����ڵ����ε�Բ�Ľ�Ϊ36�������ɼ����֣�Ƶ����
��� | �ɼ����֣� | Ƶ�� |
A | 30��x��34 | 1 |
B | 34��x��38 | 1 |
C | 38��x��42 | 6 |
D | 42��x��46 | b |
E | 46��x��50 | 30 |
�ϼ� | a | |
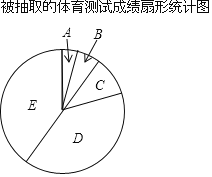
��������ͼ���ṩ����Ϣ���ش��������⣺
��1������Ƶ���ֲ�����a��b��ֵ��
��2������C��38��x��42�����м�ֵ40������C�����������ݵĺ�Ϊ�� ��
��3������ƽ�����У����ѧ���п������ɼ���ƽ���֣����ȡ��������
���𰸡���1��a=60��b��22����2��240����3����У���꼶ѧ������������Գɼ�ƽ����Լ40�֣�
��������
��1�����ȸ���Բ�ĽǵĶ���=360����ٷֱȿ����C������ռ�ٷֱȣ�����������=Ƶ�����ٷֱȿɵ�����a������������ȥ�����ֵ�Ƶ���Ϳɵ�b��ֵ��
��2����������ֵ��Ƶ�����ɣ�
��3����������ƽ���������������ƽ������������������������ķ����ɵø�У���꼶ѧ������������Գɼ���ƽ���֣�
�⣺��1��a��6��![]() ��60��
��60��
b��60����1+1+6+30����22��
��2��40��6��240��
�ʴ�Ϊ��240��
��3�������⣺![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
��![]() ���֣���
���֣���
����������ƽ���������������ƽ���֣�
��˸�У���꼶ѧ������������Գɼ�ƽ����Լ40�֣�


 ���⿼����Ԫ���Ծ�ϵ�д�
���⿼����Ԫ���Ծ�ϵ�д� ��У���˳�̾�ϵ�д�
��У���˳�̾�ϵ�д� ��У���һ��ͨϵ�д�
��У���һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����MON��45�����߶�AB������ON���˶���AB��2��
��1����ͼ1����֪OA��AB��AC��BC����ACB��90������C�ڡ�MON�ڣ�
����֤���Ե�CΪԲ�ģ�CA�İ뾶��Բ������OM���У��е��Ϊ��P����
�ڡ�APB�Ĵ�СΪ�� ����
��2����ͼ2��������OM�ϴ��ڵ�Q��ʹ�á�AQB��30�ȣ�������ͼ2����A��O����֮�����t��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
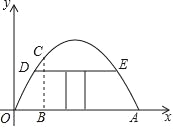
����Ŀ����һ�����������߲˴��������������ͼ��ʾ��ƽ��ֱ������ϵ�У������߿����ú���y��ax2+bx����ʾ����֪OA��8�ף�����O��2�״������BCΪ![]() �ף�
�ף�
��1����������ߵĽ���ʽ��
��2������������DE��DE��OA����һ���ţ�Ҫ���ŵĸ߶�Ϊ1.5�ף������DE�ij����Ƕ����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
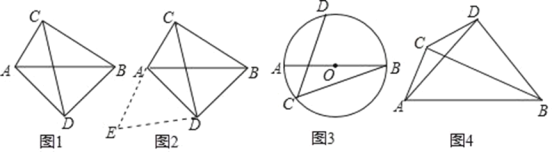
����Ŀ�������ⱳ������ͼ1,���ı���ADBC��,��ACB=��ADB=90o��AD=BD�� ̽���߶�AC��BC��CD֮���������ϵ
С��ͬѧ̽���������˼·�ǣ�����BCD�Ƶ�D,��ʱ����ת90o����AED��,��B,C�ֱ� ���ڵ�A,E��(��ͼ2),��֤��C,A,E��ͬһ��ֱ����,���ҡ�CDE�ǵ���ֱ��������,����CE=![]() CD,�Ӷ��ó����ۣ�AC+BC=
CD,�Ӷ��ó����ۣ�AC+BC= ![]() CD
CD
����Ӧ�ã�
(1)��ͼ1��,��AC=6,CD=![]() ����AB= .
����AB= .
(2)��ͼ3,AB�ǡ�O��ֱ��,��C.D�ڡ�O��,��C=45o����AB=25��BC=24����CD�ij���
����չ���죩
(3)��ͼ4,��ACB=��ADB=90o,AD=BD,��AC=![]() ,CD=
,CD=![]() ,��BC�ij�.(�ú�
,��BC�ij�.(�ú�![]() ,
,![]() �Ĵ���ʽ��ʾ)
�Ĵ���ʽ��ʾ)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����״��ͼ�����������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .Ҫ����������н�ȡһ����β��ϣ�����һ����
.Ҫ����������н�ȡһ����β��ϣ�����һ����![]() �ϣ���ʹ���ؾ��ε���������ܴ�.
�ϣ���ʹ���ؾ��ε���������ܴ�.
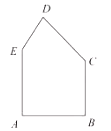
��1�������ؾ��β��ϵ�һ������![]() ��
��![]() ������β��ϵ������
������β��ϵ������
��2���ܷ�س��ȣ�1�����������ľ��β��ϣ�����ܣ������Щ���β�����������ֵ��������ܣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+![]() ��x�ύ�ڵ�A����5��0����B��1��0��������ΪD����y�ύ�ڵ�C��
��x�ύ�ڵ�A����5��0����B��1��0��������ΪD����y�ύ�ڵ�C��
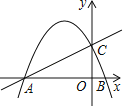
��1���������ߵı���ʽ��D�����ꣻ
��2����ֱ��AC�Ϸ������������Ƿ���ڵ�E��ʹ�á�ECA��2��CAB��������������ĵ�E�������ACE�������������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У�P��AD���е㣬��BP����A��BP�Ĵ��ߣ�����ΪF����BD��E����CD��G��
��1��������ABCD�������Σ���ͼ1��
����֤��AG��BP��
��![]() ��ֵΪ�� ����
��ֵΪ�� ����
��2����ȣ���ͼ2���ھ���ABCD�У���2AB��3AD����![]() ��ֵ��
��ֵ��
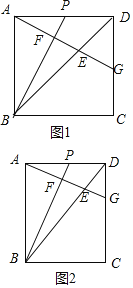
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ⱳ�������Ķ�������������⣬�ٰ�Ҫ�����������⣺
���⣺��һԪ���β���ʽx2��4��0
������������x2��4����x+2����x��2��
��x2��4��0�ɻ�Ϊ��x+2����x��2����0
���������ij˷�������������ˣ�ͬ�ŵ���������
![]()
![]()
�ⲻ��ʽ��٣���x��2��
�ⲻ��ʽ��ڣ���x����2��
�ࣨx+2����x��2����0�Ľ⼯Ϊx��2��x����2��
��һԪ���β���ʽ x2��4��0 �Ľ⼯Ϊx��2��x����2��
������Ӧ�ã���1��һԪ���β���ʽ x2��16��0 �Ľ⼯Ϊ�� ����
��2����ʽ����ʽ![]() ��0 �Ľ⼯Ϊ�� ����
��0 �Ľ⼯Ϊ�� ����
��3������չӦ�ã���һԪ���β���ʽ 2x2��3x��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������ĺ����У�װ��2�������1��������Щ�����ɫ�������ͬ.
(1)��ͬ������˵������˵������.
�ٽ��Ⱥ������������һ�����ǰ�����Ǻ������������������������������¼��ǵȿ��ܵ�.
������������ĵ�һ����Żؽ��Ⱥ��������ڶ�������������Ϳ��ܳ���3�ֽ�����������Ǻ������������ǰ���������һ��һ����.�������¼������ĸ������.
(2)���Ⱥ������������һ����Ҫʹ��������ĸ���Ϊ![]() ��Ӧ������Ӻ���
��Ӧ������Ӻ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com