
【题目】一个不透明的盒子中,装有2个白球和1个红球,这些球除颜色外其余都相同.
(1)你同意下列说法吗?请说明理由.
①搅匀后从中任意摸出一个球,不是白球就是红球,因此摸出白球和摸出红球这两个事件是等可能的.
②如果将摸出的第一个球放回搅匀后再摸出第二个球,两次摸球就可能出现3种结果,即“都是红球”、“都是白球”、“一红一白”.这三个事件发生的概率相等.
(2)搅匀后从中任意摸出一个球,要使摸出红球的概率为![]() ,应如何添加红球?
,应如何添加红球?
【答案】(1)①不同意.理由见解析;②不同意,理由见解析;(2)应添加5个红球.
【解析】
(1)①根据概率的求法,即出现的次数与总次数的比值,可以判定方法正确性;②首先根据题意画出树状图,然后由树状图求得“都是红球”、“都是白球”、“一红一白”这三个事件发生的概率,则可求得答案;
(2) 设添加红球x个,根据红球的概率公式列方程即可求出红球个数.
解:(1)①不同意.
因为摸出白球的概率是![]() ,摸出红球的概率是
,摸出红球的概率是![]() ,
,
所以摸出白球和摸出红球不是等可能的.
②不同意.
所有等可能的结果,用树状图分析如下:
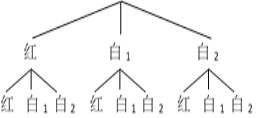
由图可知共有9种等可能的结果.
P(两红)=![]() ,P(两白)=
,P(两白)=![]() ,P(一红一白)=
,P(一红一白)=![]() .
.
(2)设应添加x个红球,由题意,得![]() .
.
解得x=5(经检验是原方程的解)
答:应添加5个红球.


科目:初中数学 来源: 题型:
【题目】为了解今年我校初三学生中考体育测试成绩,现对今年我校初三中考体育测试成绩进行抽样调查,结果统计如下,其中扇形统计图中C组所在的扇形的圆心角为36°,组别成绩(分)频数.
组别 | 成绩(分) | 频数 |
A | 30<x≤34 | 1 |
B | 34<x≤38 | 1 |
C | 38<x≤42 | 6 |
D | 42<x≤46 | b |
E | 46<x≤50 | 30 |
合计 | a | |
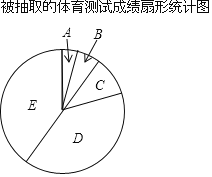
根据上面图标提供的信息,回答下列问题:
(1)计算频数分布表中a与b的值;
(2)根据C组38<x≤42的组中间值40,估计C组中所有数据的和为 ;
(3)请估计今年我校初三学生中考体育成绩的平均分(结果取整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】6月电商的“年中大促销”已开始预热,实体店也摩拳擦掌提前备战,积极展开促销活动.陈阿姨参加了某店“砸金蛋赢优惠”活动,该店提供四个外观一样的“金蛋”,每个“金蛋”内装一张优惠券,分别是10,20,50,100(单位:元)的优惠券.四个“金蛋”内的优惠券不重复.砸到哪个“金蛋”就会获得“金蛋”内相应的优惠券.
(1)如果随机砸1个“金蛋”,求陈阿姨得到100元优惠券的概率;
(2)如果随机砸2个“金蛋”,且第一次砸过的“金蛋”不能再砸第二次,请用列表或画树状图的方法求出陈阿姨所获优惠券总值不低于70元的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂大门是抛物线形水泥建筑,大门地面路宽为6![]() ,顶部距离地面的高度为4
,顶部距离地面的高度为4![]() ,现有一辆装载大型设备的车辆要进入厂区,已知设备总宽为2.4
,现有一辆装载大型设备的车辆要进入厂区,已知设备总宽为2.4![]() ,要想通过此门,则设备及车辆总高度应小于______.
,要想通过此门,则设备及车辆总高度应小于______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店经营某种品牌的文具盒,购进时的单价是30元,根据统计调查:在一段时间内,销售单价是40元时,文具盒销售量是600个,而销售单价每涨2元,就会少售出20个文具盒.
(1)不妨设该种品牌文具盒的销售单价为![]() 元(
元(![]() ),请你分别用
),请你分别用![]() 的代数式来表示销售量
的代数式来表示销售量![]() 个和销售该品牌文具盒获得利润
个和销售该品牌文具盒获得利润![]() 元,并把结果填写在表格中:
元,并把结果填写在表格中:
销售单价(元) |
|
销售量 | __________________ |
销售文具盒获得利润 | ____________________ |
(2)在(1)问条件下,若该文具店获得了6000元销售利润,求该文具盒销售单价![]() 应定为多少元?
应定为多少元?
(3)在(1)问条件下,若厂家规定该品牌文具盒销售单价不低于44元,且文具店要完成不少于380个的销售目标,求该文具店销售该品牌文具盒获得的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
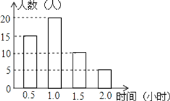
【题目】某校为了解全校2000名学生的课外阅读情况,在全校范围内随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,将结果绘制成频数分布直方图(如图所示).
(1)请分别计算这50名学生在这一天课外阅读所用时间的众数、中位数和平均数;
(2)请你根据以上调查,估计全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为O直径,点C为圆上一点,将劣弧AC沿弦AC翻折交AB于点D,连接CD,若点D与圆心O不重合,∠BAC=20°,则∠DCA的度数是()
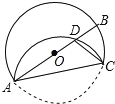
A.30°B.40°C.50°D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
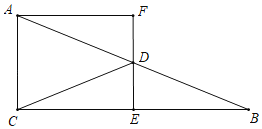
【题目】Rt△ABC中,∠ACB=90°,点D是AB中点,连CD,过点D作DE⊥BC于E,过A作AF⊥ED的延长线于F.
(1)若∠B=25°,求∠ADC的度数;
(2)求证:DF=DE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com