【题目】平面上5个圆最多能把平面分成多少个部分？一般地，n个圆最多能把平面分成多少个部分？
【答案】5个圆最多将平面分成22个部分，n个圆最多分平面为n2﹣n+2．
【解析】
根据题意，探索出圆的个数与分成的平面个数的关系，从而得出结论.
1个圆最多能把平面分成2个部分，
2个圆最多能把平面分成4个部分；
3个圆最多能把平面分成8个部分；
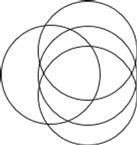
现在加入第4个圆，为了使分成的部分最多，第4个圆必须与前面3个圆都有两个交点，
如图所示，因此得6个交点将第4个圆的圆周分成6段圆弧，而每一段圆弧将原来的部分一分为二，即增加了一个部分，于是4个圆最多将平面分成8+6＝14个部分，
同理，5个圆最多将平面分成14+8＝22个部分，
一般地，n个圆最多分平面为：
2+1×2+2×2+…+（n﹣1）×2，
＝2+2[1+2+…+（n﹣1）]，
＝n2﹣n+2．
科目：初中数学 来源： 题型：
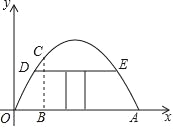
【题目】有一个抛物线型蔬菜大棚，将其截面放在如图所示的平面直角坐标系中，抛物线可以用函数y＝ax2+bx来表示，已知OA＝8米，距离O点2米处的棚高BC为
米．
（1）求该抛物线的解析式；
（2）若借助横梁DE（DE∥OA）建一个门，要求门的高度为1.5米，求横梁DE的长度是多少米？
查看答案和解析>>
科目：初中数学 来源： 题型：
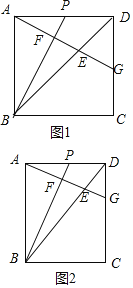
【题目】在矩形ABCD中，P是AD的中点，连BP，过A作BP的垂线，垂足为F，交BD于E，交CD于G．
（1）若矩形ABCD是正方形，如图1，
①求证：AG＝BP．
②
的值为 ．
（2）类比：如图2，在矩形ABCD中，若2AB＝3AD，求的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（问题背景）先阅读理解下面的例题，再按要求解答下列问题：
例题：解一元二次不等式x2﹣4＞0
（问题解决）∵x2﹣4＝（x+2）（x﹣2）
∴x2﹣4＞0可化为（x+2）（x﹣2）＞0
由有理数的乘法法则“两数相乘，同号得正”，得
解不等式组①，得x＞2，
解不等式组②，得x＜﹣2，
∴（x+2）（x﹣2）＞0的解集为x＞2或x＜﹣2，
即一元二次不等式 x2﹣4＞0 的解集为x＞2或x＜﹣2．
（问题应用）（1）一元二次不等式 x2﹣16＞0 的解集为 ；
（2）分式不等式
＞0 的解集为 ；
（3）（拓展应用）解一元二次不等式 2x2﹣3x＜0．
查看答案和解析>>
科目：初中数学 来源： 题型：
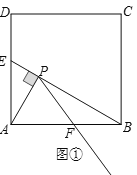
【题目】如图，正方形ABCD的边长是6，点E、F分别是边AD、AB的点,AP⊥BE于点P.
(1)如图①，当AE=2
且AF=BF时，若点T是射线PF上的一个动点(点T不与点P重合)，当△ABT是直角三角形时，求AT的长.
(2)如图②，当AE=AF时，连结CP，判断CP与PF的位置关系，并加以证明.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛一枚均匀硬币正面朝上的概率为
，下列说法错误的是
A. 连续抛一枚均匀硬币2次必有1次正面朝上
B. 连续抛一枚均匀硬币10次都可能正面朝上
C. 大量反复抛一枚均匀硬币，平均每100次出现正面朝上50次
D. 通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】矩形ABCD与CEFG，如图放置，点B，C，E共线，点C，D，G共线，连接AF，取AF的中点H，连接GH．若BC=EF=2，CD=CE=1，则GH=（ ）
A. 1 B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个不透明的盒子中，装有2个白球和1个红球，这些球除颜色外其余都相同.
(1)你同意下列说法吗？请说明理由.
①搅匀后从中任意摸出一个球，不是白球就是红球，因此摸出白球和摸出红球这两个事件是等可能的.
②如果将摸出的第一个球放回搅匀后再摸出第二个球，两次摸球就可能出现3种结果，即“都是红球”、“都是白球”、“一红一白”.这三个事件发生的概率相等.
(2)搅匀后从中任意摸出一个球，要使摸出红球的概率为
，应如何添加红球？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线y＝3x2+bx+c与直线y＝﹣1只有一个公共点M，与平行于x轴的直线l交此抛物线A，B两点若AB=4，则点M到直线l的距离为（ ）
A.11B.12C.
D.13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com