
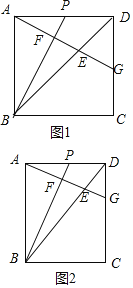
【题目】在矩形ABCD中,P是AD的中点,连BP,过A作BP的垂线,垂足为F,交BD于E,交CD于G.
(1)若矩形ABCD是正方形,如图1,
①求证:AG=BP.
②![]() 的值为 .
的值为 .
(2)类比:如图2,在矩形ABCD中,若2AB=3AD,求![]() 的值.
的值.
【答案】(1)①详见解析;②![]() ;(2)
;(2)![]() .
.
【解析】
(1)①由题意可证△ABP≌△ADG,可得AG=BP;
②由△ABP≌△ADG可得AP=DG=![]() AB,根据平行线分线段成比例可得
AB,根据平行线分线段成比例可得![]() 的值;
的值;
(2)由题意可证△ABP∽△ADG,可得2AP=3DG,即可得AD=3DG,2AB=9DG,根据平行线分线段成比例可得![]() 的值.
的值.
解:(1)证明:∵四边形ABCD是正方形
∴∠BAD=∠ADC=90° AB=AD
∴∠BAG+∠DAG=90°
∵AG⊥BP
∴∠BAG+∠ABP=90°
∴∠DAG=∠ABP且AB=AD,∠BAD=∠ADG
∴△BAP≌△ADG
∴AG=BP
(2)∵△BAP≌△ADG
∴AP=DG
∵点P是AD中点
∴AP=![]() AD=
AD=![]() AB
AB
∴DG=![]() AB
AB
∵AB∥CD
![]()
故答案为![]()
(3)∵四边形ABCD是矩形
∴∠BAD=∠ADC=90° AB∥CD
∴∠BAG+∠DAG=90°
∵AG⊥BP
∴∠BAG+∠ABP=90°
∴∠DAG=∠ABP,∠BAD=∠ADG
∴△BAP∽△ADG
![]()
∵2AB=3AD
![]()
∴2AP=3DG
∵P点是AD中点
∴AD=2AP
∴AD=3DG
∵2AB=3AD
∴2AB=9DG
∵AB∥CD
![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
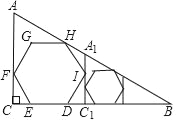
【题目】如图,Rt△ABC中,∠C=Rt∠,AB=2,∠B=30°,正六边形DEFGHI完全落在Rt△ABC内,且DE在BC边上,F在AC边上,H在AB边上,则正六边形DEFGHI的边长为_____,过I作A1C1∥AC,然后在△A1C1B内用同样的方法作第二个正六边形,按照上面的步骤继续下去,则第n个正六边形的边长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点都在格点上.
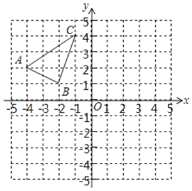
(1)请按下列要求画图:
①将△ABC先向右平移5个单位,再向上平移1个单位,得到△A1B1C1,画出△A1B1C1;
②△A2B2C2与△ABC关于原点O成中心对称,画出△A2B2C2;
(2)若(1)所得的△A1B1C1与△A2B2C2,关于点P成中心对称,直接写出对称中心P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解今年我校初三学生中考体育测试成绩,现对今年我校初三中考体育测试成绩进行抽样调查,结果统计如下,其中扇形统计图中C组所在的扇形的圆心角为36°,组别成绩(分)频数.
组别 | 成绩(分) | 频数 |
A | 30<x≤34 | 1 |
B | 34<x≤38 | 1 |
C | 38<x≤42 | 6 |
D | 42<x≤46 | b |
E | 46<x≤50 | 30 |
合计 | a | |
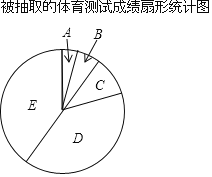
根据上面图标提供的信息,回答下列问题:
(1)计算频数分布表中a与b的值;
(2)根据C组38<x≤42的组中间值40,估计C组中所有数据的和为 ;
(3)请估计今年我校初三学生中考体育成绩的平均分(结果取整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=ax2+bx+c(a≠0)的图象如图,下列5个结论,其中正确的结论有( )
①abc<0
②3a+c>0
③4a+2b+c<0
④2a+b=0
⑤b2>4ac
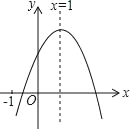
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
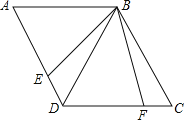
【题目】(1)解方程:x2﹣5=4x.
(2)如图,四边形ABCD中,∠C=60°,∠BED=110°,BD=BC,点E在AD上,将BE绕点B逆时针旋转60°得BF,且点F在DC上,求∠EBD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
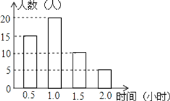
【题目】某校为了解全校2000名学生的课外阅读情况,在全校范围内随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,将结果绘制成频数分布直方图(如图所示).
(1)请分别计算这50名学生在这一天课外阅读所用时间的众数、中位数和平均数;
(2)请你根据以上调查,估计全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com