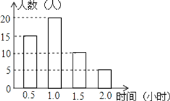
【题目】某校为了解全校2000名学生的课外阅读情况，在全校范围内随机调查了50名学生，得到他们在某一天各自课外阅读所用时间的数据，将结果绘制成频数分布直方图（如图所示）．
（1）请分别计算这50名学生在这一天课外阅读所用时间的众数、中位数和平均数；
（2）请你根据以上调查，估计全校学生中在这一天课外阅读所用时间在1.0小时以上（含1.0小时）的有多少人？
科目：初中数学 来源： 题型：
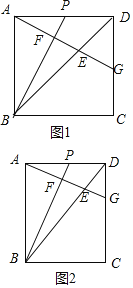
【题目】在矩形ABCD中，P是AD的中点，连BP，过A作BP的垂线，垂足为F，交BD于E，交CD于G．
（1）若矩形ABCD是正方形，如图1，
①求证：AG＝BP．
②
的值为 ．
（2）类比：如图2，在矩形ABCD中，若2AB＝3AD，求的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】矩形ABCD与CEFG，如图放置，点B，C，E共线，点C，D，G共线，连接AF，取AF的中点H，连接GH．若BC=EF=2，CD=CE=1，则GH=（ ）
A. 1 B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个不透明的盒子中，装有2个白球和1个红球，这些球除颜色外其余都相同.
(1)你同意下列说法吗？请说明理由.
①搅匀后从中任意摸出一个球，不是白球就是红球，因此摸出白球和摸出红球这两个事件是等可能的.
②如果将摸出的第一个球放回搅匀后再摸出第二个球，两次摸球就可能出现3种结果，即“都是红球”、“都是白球”、“一红一白”.这三个事件发生的概率相等.
(2)搅匀后从中任意摸出一个球，要使摸出红球的概率为
，应如何添加红球？
查看答案和解析>>
科目：初中数学 来源： 题型：
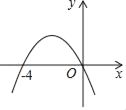
【题目】如图是二次函数y＝ax2+bx+c（a≠0）的图象与x轴的相交情况，关于下列结论：
①方程ax2+bx＝0的两个根为x1＝0，x2＝﹣4；②b﹣4a＝0；③9a+3b+c＜0；其中正确的结论有（ ）
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：对于给定的两个函数,任取自变量x的一个值,当x<0时,它们对应的函数值互为相反数;当x0时,它们对应的函数值相等,我们称这样的两个函数互为相关函数。例如：一次函数y=x1,它们的相关函数为y=
.
(1)已知点A(5,8)在一次函数y=ax3的相关函数的图象上，求a的值；
(2)已知二次函数y=x
+4x
.
①当点B(m,
)在这个函数的相关函数的图象上时，求m的值；
②当3x3时,求函数y=x+4x的相关函数的最大值和最小值.
查看答案和解析>>
科目：初中数学 来源： 题型：
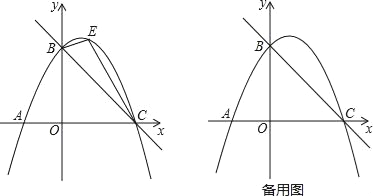
【题目】如图，直线y＝﹣2x+3与x轴交于点C，与y轴交于点B，抛物线y＝ax2+x+c经过B、C两点．
(1)求抛物线的解析式；
(2)如图，点E是直线BC上方抛物线上的一动点，当△BEC面积最大时，请求出点E的坐标和△BEC面积的最大值？
(3)在(2)的结论下，过点E作y轴的平行线交直线BC于点M，连接AM，点Q是抛物线对称轴上的动点，在抛物线上是否存在点P，使得以P、Q、A、M为顶点的四边形是平行四边形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线y＝3x2+bx+c与直线y＝﹣1只有一个公共点M，与平行于x轴的直线l交此抛物线A，B两点若AB=4，则点M到直线l的距离为（ ）
A.11B.12C.
D.13
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】花园小区有一朝向为正南方向的居民楼（如图），该居民楼的一楼是高4米的小区商场，商场以上是居民住房．在该楼的前面16米处要盖一栋高18米的办公楼．当冬季正午的阳光与水平线的夹角为
时，问：
（1）商场以上的居民住房采光是否有影响，为什么？
（2）若要使商场采光不受影响，两楼应相距多少 米？（结果保留一位小数）
（参考数据：
，
，
）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
