
【题目】定义:对于给定的两个函数,任取自变量x的一个值,当x<0时,它们对应的函数值互为相反数;当x0时,它们对应的函数值相等,我们称这样的两个函数互为相关函数。例如:一次函数y=x1,它们的相关函数为y=![]() .
.
(1)已知点A(5,8)在一次函数y=ax3的相关函数的图象上,求a的值;
(2)已知二次函数y=x![]() +4x
+4x![]() .
.
①当点B(m,![]() )在这个函数的相关函数的图象上时,求m的值;
)在这个函数的相关函数的图象上时,求m的值;
②当3x3时,求函数y=x![]() +4x
+4x![]() 的相关函数的最大值和最小值.
的相关函数的最大值和最小值.
【答案】(1)1;(2)①m=2![]() 或m=2+
或m=2+![]() 或m=2
或m=2![]() ;②最大值为
;②最大值为![]() ,最小值为
,最小值为![]() .
.
【解析】
(1)写出y=ax-3的相关函数,代入计算;
(2)①写出二次函数y=x![]() +4x
+4x![]() 的相关函数,代入计算;
的相关函数,代入计算;
②根据二次根式的最大值和最小值的求法解答.
(1)y=ax3的相关函数y=![]() ,
,
将A(5,8)代入y=ax+3得:5a+3=8,
解得a=1;
(2)二次函数y=x![]() +4x
+4x![]() 的相关函数为y=
的相关函数为y=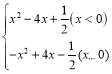 ,
,
①当m<0时,将B(m, ![]() )代入y=x
)代入y=x![]() -4x+
-4x+![]()
得m![]() -4m+
-4m+![]() ,
,
解得:m=2+![]() (舍去),或m=2
(舍去),或m=2![]() ,
,
当m0时,将B(m,![]() )代入y=x
)代入y=x![]() +4x
+4x![]() 得:
得:
m![]() +4m
+4m![]() ,
,
解得:m=2+![]() 或m=2
或m=2![]() .
.
综上所述:m=2![]() 或m=2+
或m=2+![]() 或m=2
或m=2![]() ;
;
②当3x<0时, y=x![]() +4x
+4x![]() ,抛物线的对称轴为x=2,
,抛物线的对称轴为x=2,
此时y随x的增大而减小,
∴此时y的最大值为![]() ,
,
当0x3时,函数y=x![]() +4x
+4x![]() ,抛物线的对称轴为x=2,
,抛物线的对称轴为x=2,
当x=0有最小值,最小值为![]() ,当x=2时,有最大值,最大值y=
,当x=2时,有最大值,最大值y=![]() ,
,
综上所述,当3x3时,函数y=x![]() +4x
+4x![]() 的相关函数的最大值为
的相关函数的最大值为![]() ,最小值为
,最小值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数![]() 的图象和性质进行了探究,探究过程如下:
的图象和性质进行了探究,探究过程如下:
(![]() )自变量
)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值如下表:
的几组对应值如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() __________.
__________.
(![]() )根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请你画出该函数图象剩下的部分.
)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请你画出该函数图象剩下的部分.

(![]() )观察函数图象,写出一条性质__________.
)观察函数图象,写出一条性质__________.
(![]() )进一步探究函数图象发现:
)进一步探究函数图象发现:
①方程![]() 有__________个实数根.
有__________个实数根.
②关于![]() 的方程
的方程![]() 有
有![]() 个实数根时,
个实数根时,![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小明家的住房结构平面图(单位:米),他打算把卧室以外的部分都铺上地砖.

(1)若铺地砖的价格为80元/平方米,那么铺地砖需要花多少钱?(用代数式表示)
(2)已知房屋的高为h米,现需要在客厅和卧室的墙壁上贴壁纸,那么需要多少平方米的壁纸(计算时不扣除门,窗所占的面积)?(用代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]()
![]() 的对称轴为直线
的对称轴为直线![]() ,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:
,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:
①抛物线过原点;②a-b+c<0;③当x<1时,y随x增大而增大;
④抛物线的顶点坐标为(2,b);⑤若ax2+bx+c=b,则b2-4ac=0.
其中正确的是( )

A. ①②③ B. ①④⑤ C. ①②④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举行春季长跑比赛活动,小明从起点学校西门出发,途经市博物馆后按原路返还,沿比赛路线跑回终点学校西门.设小明离开起点的路程s(千米)与跑步时间t(分钟)之间的函数关系如图所示,其中从起点到市博物馆的平均速度是0.3千米/分钟,用时35分钟根据图象提供的信息,解答下列问题:

(1)求图中![]() 的值,并求出
的值,并求出![]() 所在直线方程;
所在直线方程;
(2)组委会在距离起点2.1千米处设立一个拍摄点![]() ,小明从第一次过点
,小明从第一次过点![]() 到第二次经过点
到第二次经过点![]() 所用的时间为68分钟
所用的时间为68分钟
①求![]() 所在直线的函数解析式;
所在直线的函数解析式;
②该运动员跑完赛程用时多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD内找一点O,使它到四边形四个顶点的距离之和OA+OB+OC+OD最小,正确的作法是连接AC、BD交于点O,则点O就是要找的点,请你用所学过的数学知识解释这一道理__________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知双曲线![]() ,经过点D(6,1),点C是双曲线第三象限上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
,经过点D(6,1),点C是双曲线第三象限上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
(1)求k的值;
(2)若△BCD的面积为12,求直线CD的解析式;
(3)判断AB与CD的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下4个图中,不同的矩形ABCD,若把D点沿AE对折,使D点与BC上的F点重合;
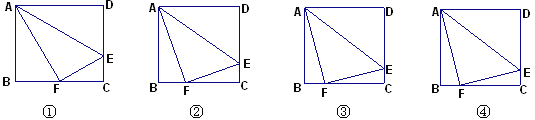
(1)图①中,若DE︰EC=2︰1,求证:△ABF∽△AFE∽△FCE;并计算BF︰FC;
(2)图②中若DE︰EC=3︰1,计算BF︰FC= ;图③中若DE︰EC=4︰1,计算BF︰FC= ;
(3)图④中若DE︰EC=![]() ︰1,猜想BF︰FC= ;并证明你的结论
︰1,猜想BF︰FC= ;并证明你的结论
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完。设分配给甲店A型产品x件,两商店销售这两种产品每件的利润(元)如下表:
A型利润 | B型利润 | |
甲店 | 200 | 170 |
乙店 | 160 | 150 |
(1)分配给乙店B型产品 件(用含x的代数式表示)。
(2)设这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并直接写出x的取值范围。
(3)若公司要求总利润不低于17560元,有几种不同分配方案?哪种方案总利润最大?请求出最大利润。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com