
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点都在格点上.
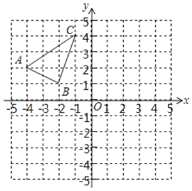
(1)请按下列要求画图:
①将△ABC先向右平移5个单位,再向上平移1个单位,得到△A1B1C1,画出△A1B1C1;
②△A2B2C2与△ABC关于原点O成中心对称,画出△A2B2C2;
(2)若(1)所得的△A1B1C1与△A2B2C2,关于点P成中心对称,直接写出对称中心P点的坐标.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( )
的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( )
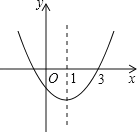
A.abc<0B.2a+b<0C.a-b+c<0D.4ac-b2<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线C1:y=ax2+bx+c(a>0)与x轴交于点(﹣1,0),(2,0).
(1)b、c分别用含a的式子表示为:b= ,c= ;
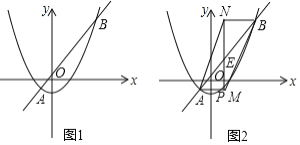
(2)将抛物线C1向左平移![]() 个单位,得到抛物线C2.直线y=kx+a(k>0)与C2交于A,B两点(A在B左侧).P是抛物线C2上一点,且在直线AB下方.作PE∥y轴交线段AB于E,过A、B两点分别作PE的垂线AM、BN,垂足分别为M,N.
个单位,得到抛物线C2.直线y=kx+a(k>0)与C2交于A,B两点(A在B左侧).P是抛物线C2上一点,且在直线AB下方.作PE∥y轴交线段AB于E,过A、B两点分别作PE的垂线AM、BN,垂足分别为M,N.
①当P点在y轴上时,试说明:AMBN为定值.
②已知当点P(a,n)时,恰有S△ABM=S△ABN,求当1≤a≤3时,k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
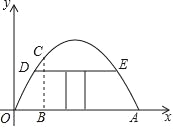
【题目】有一个抛物线型蔬菜大棚,将其截面放在如图所示的平面直角坐标系中,抛物线可以用函数y=ax2+bx来表示,已知OA=8米,距离O点2米处的棚高BC为![]() 米.
米.
(1)求该抛物线的解析式;
(2)若借助横梁DE(DE∥OA)建一个门,要求门的高度为1.5米,求横梁DE的长度是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
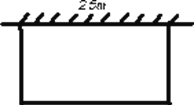
【题目】如图,利用一面长![]() 的墙,用
的墙,用![]() 长的篱笆,围成一个长方形的养鸡场.
长的篱笆,围成一个长方形的养鸡场.
(1)怎样围成一个面积为![]() 的长方形养鸡场?
的长方形养鸡场?
(2)能否围成一个面积为![]() 的长方形养鸡场?如能,说明围法;如不能,请说明理由.
的长方形养鸡场?如能,说明围法;如不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
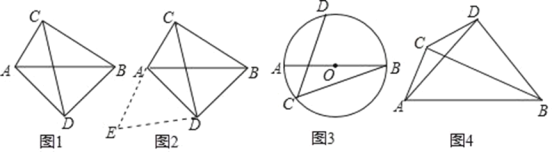
【题目】(问题背景)如图1,在四边形ADBC中,∠ACB=∠ADB=90o,AD=BD, 探究线段AC,BC,CD之间的数量关系
小明同学探究此问题的思路是:将△BCD绕点D,逆时针旋转90o到△AED处,点B,C分别 落在点A,E处(如图2),易证点C,A,E在同一条直线上,并且△CDE是等腰直角三角形,所以CE=![]() CD,从而得出结论:AC+BC=
CD,从而得出结论:AC+BC= ![]() CD
CD
(简单应用)
(1)在图1中,若AC=6,CD=![]() ,则AB= .
,则AB= .
(2)如图3,AB是⊙O的直径,点C.D在⊙O上,∠C=45o,若AB=25,BC=24,求CD的长.
(拓展延伸)
(3)如图4,∠ACB=∠ADB=90o,AD=BD,若AC=![]() ,CD=
,CD=![]() ,求BC的长.(用含
,求BC的长.(用含![]() ,
,![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
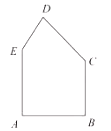
【题目】有一块形状如图的五边形余料![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .要在这块余料中截取一块矩形材料,其中一边在
.要在这块余料中截取一块矩形材料,其中一边在![]() 上,并使所截矩形的面积尽可能大.
上,并使所截矩形的面积尽可能大.
(1)若所截矩形材料的一条边是![]() 或
或![]() ,求矩形材料的面积;
,求矩形材料的面积;
(2)能否截出比(1)中面积更大的矩形材料?如果能,求出这些矩形材料面积的最大值,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
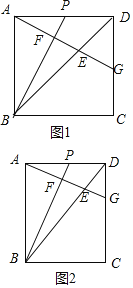
【题目】在矩形ABCD中,P是AD的中点,连BP,过A作BP的垂线,垂足为F,交BD于E,交CD于G.
(1)若矩形ABCD是正方形,如图1,
①求证:AG=BP.
②![]() 的值为 .
的值为 .
(2)类比:如图2,在矩形ABCD中,若2AB=3AD,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD与CEFG,如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=( )

A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com