
【题目】已知:抛物线C1:y=ax2+bx+c(a>0)与x轴交于点(﹣1,0),(2,0).
(1)b、c分别用含a的式子表示为:b= ,c= ;
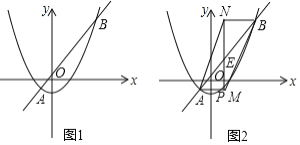
(2)将抛物线C1向左平移![]() 个单位,得到抛物线C2.直线y=kx+a(k>0)与C2交于A,B两点(A在B左侧).P是抛物线C2上一点,且在直线AB下方.作PE∥y轴交线段AB于E,过A、B两点分别作PE的垂线AM、BN,垂足分别为M,N.
个单位,得到抛物线C2.直线y=kx+a(k>0)与C2交于A,B两点(A在B左侧).P是抛物线C2上一点,且在直线AB下方.作PE∥y轴交线段AB于E,过A、B两点分别作PE的垂线AM、BN,垂足分别为M,N.
①当P点在y轴上时,试说明:AMBN为定值.
②已知当点P(a,n)时,恰有S△ABM=S△ABN,求当1≤a≤3时,k的取值范围.
【答案】(1)﹣a,﹣2a;(2)①见解析;②2≤k≤18.
【解析】
(1)根据抛物线的表达式为:y=a(x+1)(x﹣2)=ax2﹣ax﹣2a即可求解;
(2)①由(1)知,b=﹣a,c=﹣2a,抛物线C1的表达式为:y=ax2﹣ax﹣2a=a(x﹣![]() )2﹣
)2﹣![]() ,则抛物线C2的表达式为:y=ax2﹣
,则抛物线C2的表达式为:y=ax2﹣![]() ,联立直线与抛物线C2的表达式并整理得:ax2﹣kx﹣
,联立直线与抛物线C2的表达式并整理得:ax2﹣kx﹣![]() =0,即可证明AMBN为定值;
=0,即可证明AMBN为定值;
②S△ABM=S△ABN,则AM=BN,a﹣x1=x2﹣a,得到x1+x2=2a,x1+x2=![]() ,即可求出k的取值范围.
,即可求出k的取值范围.
解:根据抛物线的表达式为:y=a(x+1)(x﹣2)=ax2﹣ax﹣2a,
故b=﹣a,c=﹣2a,
故答案为﹣a,﹣2a;
(2)设:点A、B的坐标分别为:(x1,y1)、(x2,y2),
①由(1)知,b=﹣a,c=﹣2a,
抛物线C1的表达式为:y=ax2﹣ax﹣2a=a(x﹣![]() )2﹣
)2﹣![]() ,
,
则抛物线C2的表达式为:y=ax2﹣![]() ,
,
联立直线与抛物线C2的表达式并整理得:ax2﹣kx﹣![]() =0,
=0,
则x1x2=![]() =AMBN,
=AMBN,
故AMBN为定值;
②∵S△ABM=S△ABN,
∴AM=BN,a﹣x1=x2﹣a,则x1+x2=2a,
∵x1+x2=![]() ,
,
∴![]() =2a,
=2a,
∴k=2a2,
∵1≤a≤3,
∴2≤k≤18.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】计算
(1)![]()
(2)![]()
(3)(6x-1)2-25=0
(4)![]()
(5) ![]()
(6) ![]()
(7)![]() +
+![]() +(﹣1)0﹣2sin45°
+(﹣1)0﹣2sin45°
(8)6tan230°-cos30°·tan60°-2sin 45°+cos60°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形ABCD的边长为2,正方形EFGH的边长为5,点A的坐标为(﹣4,0),点E的坐标为(3,0),AB与EF均在x轴上.
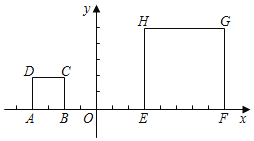
(1)C,G两点的坐标分别为 , .
(2)将正方形ABCD绕点E顺时针旋转90°得到正方形A'B'C'D',求点C'的坐标和FC'的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
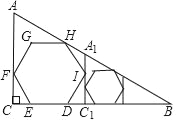
【题目】如图,Rt△ABC中,∠C=Rt∠,AB=2,∠B=30°,正六边形DEFGHI完全落在Rt△ABC内,且DE在BC边上,F在AC边上,H在AB边上,则正六边形DEFGHI的边长为_____,过I作A1C1∥AC,然后在△A1C1B内用同样的方法作第二个正六边形,按照上面的步骤继续下去,则第n个正六边形的边长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
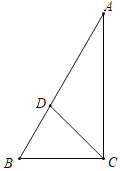
【题目】已知Rt△ABC中,∠ACB=90°,∠B=60°,BC=4,D为AB边上一点,且BD=3,将△BCD绕着点C顺时针旋转60°到△B′CD′,则AD′的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一座拱桥的轮廓是抛物线型(如图1所示),拱高6m,跨度20m,相邻两支柱间的距离均为5m.
(1)将抛物线放在所给的直角坐标系中(如图2所示),求抛物线的解析式;
(2)求支柱![]() 的长度;
的长度;
(3)拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车(汽车间的间隔忽略不计)?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学综合实践活动中,小明计划测量城门大楼的高度,在点B处测得楼顶A的仰角为22°,他正对着城楼前进21米到达C处,再登上3米高的楼台D处,并测得此时楼顶A的仰角为45°.
(1)求城门大楼的高度;
(2)每逢重大节日,城门大楼管理处都要在A,B之间拉上绳子,并在绳子上挂一些彩旗,请你求出A,B之间所挂彩旗的长度(结果保留整数).(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点都在格点上.
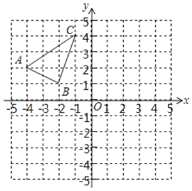
(1)请按下列要求画图:
①将△ABC先向右平移5个单位,再向上平移1个单位,得到△A1B1C1,画出△A1B1C1;
②△A2B2C2与△ABC关于原点O成中心对称,画出△A2B2C2;
(2)若(1)所得的△A1B1C1与△A2B2C2,关于点P成中心对称,直接写出对称中心P点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com