
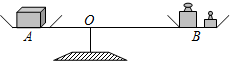
 如图,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘A中放置一个重物,在右边活动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.实验数据记录如下表:
如图,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘A中放置一个重物,在右边活动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.实验数据记录如下表:| x(cm) | 10 | 15 | 20 | 25 | 30 |
| y(g) | 30 | 20 | 15 | 12 | 10 |
分析 (1)观察可得:x,y的乘积为定值300,故y与x之间的函数关系为反比例函数,将数据代入用待定系数法可得反比例函数的关系式;
(2)把x=24代入解析式求解,可得答案;
(3)利用函数增减性即可得出,随着活动托盘B与O点的距离不断增大,砝码的示数应该不断减小.
解答 解:(1)由图象猜测y与x之间的函数关系为反比例函数,
∴设y=$\frac{k}{x}$(k≠0),
把x=10,y=30代入得:k=300,
∴y=$\frac{300}{x}$,
将其余各点代入验证均适合,
∴y与x的函数关系式为:y=$\frac{300}{x}$;
(2)把y=24代入y=$\frac{300}{x}$得:x=12.5,
∴当砝码的质量为24g时,活动托盘B与点O的距离是12.5cm.
(3)根据反比例函数的增减性,即可得出,随着活动托盘B与O点的距离不断减小,砝码的示数会不断增大;
∴应添加砝码.
点评 此题主要考查了反比例函数的应用,此题是跨学科的综合性问题,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
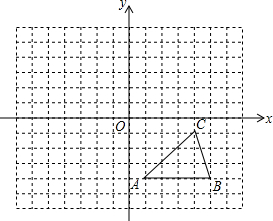 如图,在平面直角坐标系中,△ABC为格点三角形(顶点都是格点)且C(4,-1)
如图,在平面直角坐标系中,△ABC为格点三角形(顶点都是格点)且C(4,-1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
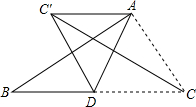 如图,AD是△ABC的边BC上的中线,且AD=BD=CD,把△ADC沿AD对折,点C落在点C′处,连接CC′,图中有哪些线段互相垂直?请一一写出来,并选择其中一组加以证明.
如图,AD是△ABC的边BC上的中线,且AD=BD=CD,把△ADC沿AD对折,点C落在点C′处,连接CC′,图中有哪些线段互相垂直?请一一写出来,并选择其中一组加以证明.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 27° | B. | 26° | C. | 23° | D. | 22° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD的对角线AC、BD相交于点E.
如图,四边形ABCD的对角线AC、BD相交于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com