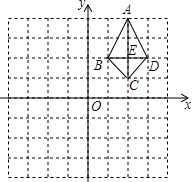练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．如图，四边形ABCD的对角线AC、BD相交于点E．
    （1）将四边形ABCD绕点E旋转180°，画出旋转后的四边形，并写出点A的对应点A′的坐标；
    （2）求四边形ABCD与旋转后的四边形重叠部分的面积．

    分析 （1）利用旋转的性质得出对应点位置进而得出答案；
    （2）利用正方形的性质与判定得出四边形ABCD与旋转后的四边形重叠部分的面积．

    解答 解：（1）如图所示：四边形A′B′C′D′即为所求，
    A′的坐标为：（2，0）；

    （2）如图所示：四边形ABCD与旋转后的四边形重叠部分是四边形C′BCD，
    四边形C′BCD是正方形，其面积是：$\sqrt{2}$×$\sqrt{2}$=2．

    点评 此题主要考查了旋转变换以及正方形的性质，根据题意得出对应点位置是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

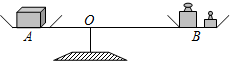    3．如图，李老师设计了一个探究杠杆平衡条件的实验：在一个自制类似天平的仪器的左边固定托盘A中放置一个重物，在右边活动托盘B（可左右移动）中放置一定质量的砝码，使得仪器左右平衡．改变活动托盘B与点O的距离x（cm），观察活动托盘B中砝码的质量y（g）的变化情况．实验数据记录如下表：
    x（cm）1015202530
    y（g）3020151210
    （1）猜测y与x之间的函数关系，求出函数关系式并加以验证；
    （2）当砝码的质量为24g时，活动托盘B与点O的距离是多少？
    （3）将活动托盘B往左移动时，应往活动托盘B中添加还是减少砝码？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．计算：
    （1）（$\sqrt{24}$-$\sqrt{\frac{1}{2}}$）-（$\sqrt{\frac{1}{8}}$+$\sqrt{6}$）；
    （2）2$\sqrt{12}$×$\frac{\sqrt{3}}{4}$÷5$\sqrt{2}$；
    （3）（2$\sqrt{3}$+6）（2$\sqrt{3}$-$\sqrt{6}$）
    （4）（2$\sqrt{48}$-3$\sqrt{27}$）$÷\sqrt{6}$
    （5）（2$\sqrt{2}$+3$\sqrt{3}$）2；
    （6）（$\frac{3}{2}$$\sqrt{1\frac{2}{3}}$-$\sqrt{1\frac{1}{4}}$）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

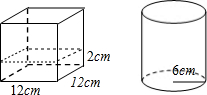    1．如图所示，一个底面为正方形的容器中盛有高度为2cm的液体，正方形的边长为12cm，把这些液体倒入底面半径为6cm的圆柱形容器中，求液体的高度．（结果保留π）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．已知二次函数y=ax2+bx+c的图象与反比例函数y=$\frac{a+3}{x}$的图象交于点A（a，-2）．
    （1）求a的值；
    （2）设这个二次函数的图象与y轴交于点B，且∠ABO=135°，求这个二次函数的图象的顶点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．某车间加工A型和B型两种零件，平均一个工人每小时能加工7个A型零件和3个B型零件，而且3个A型与2个B型配套，就可以包装进库房，剩余不能配套的只能暂时存放起来，如果B型零件单独存放，对环境的要求远高于A型零件，已知该车间原有工人69名．
    （1）怎样分配工人进行工作才能保证生产出的产品及时包装运进库房；
    （2）后来因为工作调动，有4名工人调离了该车间，那么你认为现在应该怎样分配工人工作最合适呢？请通过计算说明你的依据．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．已知4a2+b2-4a+4b+5=0，求代数式（4a-b）2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．已知：在△ABC中，BC的垂直平分线交∠BAC的外角平分线于点D，连结DC、DB．证明：∠DBA=∠DCA．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如果两个有理数a，b，同时满足下列两个条件：（1）a+b=-ab；（2）a、b同号，就称a，b互为“同伴数”．请问-$\frac{1}{2}$有“同伴数”吗？为什么？

    查看答案和解析>>

    同步练习册答案