
分析 (1)设分配加工A型零件工人为x人,加工B型零件工人为(69-x)人,分别求得生产两种类型零件的总数,根据3个A型与2个B型配套列出方程解答即可;
(2)若调走4名工人,设分配生产A型零件工人为x人,则生产B型为(65-x)人,分别求得生产两种类型零件的总数,根据3个A型与2个B型配套,且A的剩余量大于B的剩余量列出不等式解答即可.
解答 解:(1)设分配加工A型零件工人为x人,加工B型零件工人为(69-x)人,由题意得
$\frac{7}{3}$x=$\frac{3(69-x)}{2}$,
解得:x=27.
答:分配加工A型零件工人为27人,加工B型零件工人为42人.
(2)若调走4名工人,设分配生产A型零件工人为x人,则生产B型为(65-x)人,由题意得
$\frac{7}{3}$x≥$\frac{3(65-x)}{2}$,
解得:x≥25$\frac{10}{23}$,
∵x为整数,
∴x=26,
65-x=39.
答:分配加工A型零件工人为26人,加工B型零件工人为39人.
点评 此题考查一元一次不等式,一元一次方程的实际运用,找出题目蕴含的等量关系与不等关系是解决问题的关键.


科目:初中数学 来源: 题型:解答题
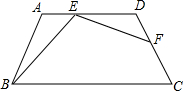 在梯形ABCD中,AD∥BC.AB=DC=AD=6,∠ABC=60°,点E、F分别在AD、DC上(点E与A、D不重合);且∠BEF=120°,设AE=x,DF=y.
在梯形ABCD中,AD∥BC.AB=DC=AD=6,∠ABC=60°,点E、F分别在AD、DC上(点E与A、D不重合);且∠BEF=120°,设AE=x,DF=y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
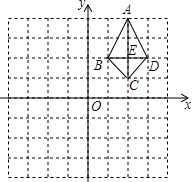 如图,四边形ABCD的对角线AC、BD相交于点E.
如图,四边形ABCD的对角线AC、BD相交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com