
【题目】某电器超市销售A、B两种不同型号的电风扇,每种型号电风扇的购买单价分别为每台310元,460元.
(1)若某单位购买A,B两种型号的电风扇共50台,且恰好支出20000元,求A,B两种型号电风扇各购买多少台?
(2)若购买A,B两种型号的电风扇共50台,且支出不超过18000元,求A种型号电风扇至少要购买多少台?
【答案】(1)购买A种型号电风扇20台,B型种型号电风扇30台;
(2)A种型号电风扇至少要购买34台
【解析】试题分析:(1)设购买A种型号电风扇x套,B型号的电风扇y套,根据:“A,B两种型号的电风扇共50套、共支出20000元”列方程组求解可得;
(2)设购买A型号电风扇m套,根据:A型电风扇总费用+B型电风扇总费用≤18000,列不等式求解可得.
试题解析:
(1)设购买A种型号电风扇x台,B种型号电风扇y台,
根据题意,得: ![]() , 解得:x=20,y=30,
, 解得:x=20,y=30,
答:购买A种型号电风扇20台,B型种型号电风扇30台.
(2)设购买A种型号电风扇m台,
根据题意,得:310m+460(50-m)≤18000,
解得:m≥33![]() ,
,
∵m为整数,∴m的最小值为34,
答:A种型号电风扇至少要购买34台.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】在2020年元月的日历表中,某一天对应的号数的上、下、左、右四个数的和为![]() .
.
(1)如果某一天是![]() 号,请用含
号,请用含 ![]() 的代数式把
的代数式把![]() 表示出来;
表示出来;
(2)![]() 的值可能是96吗?如果可能,求出这一天上、下、左、右四天,如果不可能,请说明理由;
的值可能是96吗?如果可能,求出这一天上、下、左、右四天,如果不可能,请说明理由;
(3)![]() 的值可能是28吗?如果可能,求出这一天上、下、左、右四天,如果不可能,请说明理由.
的值可能是28吗?如果可能,求出这一天上、下、左、右四天,如果不可能,请说明理由.
星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
1 | 2 | 3 | 4 | |||
5 | 6 | 7 | 8 | 9 | 10 | 11 |
12 | 13 | 14 | 15 | 16 | 17 | 18 |
19 | 21 | 22 | 23 | 24 | 25 | |
26 | 27 | 28 | 29 | 30 | 31 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市第一次用12000元购进甲、乙两种商品.其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表:
倍多15件,甲、乙两种商品的进价和售价如下表:
甲 | 乙 | |
进价(元件) | 44 | 60 |
售价(元件) | 58 | 80 |
(1)该超市第一次购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多360元,求第二次乙商品是按原价打几折销售?(提示:设原价打![]() 折销售,则实际售价=原价
折销售,则实际售价=原价![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点A,B对应的数分别是﹣10,8,P,Q,N为数轴上三个动点,点P从点A出发速度为每秒2个单位,点Q从点B出发,速度为点P的2倍,点N从原点出发,速度为每秒1个单位.
(1)若P,Q两点不动,动点N是线段AB的三等分点时,点N所表示的数是 ;
(2)若点P向左运动,同时点Q向右运动,求多长时间点P与点Q相距32个单位?
(3)若点P,Q,N同时都向右运动求多长时间点N到点P和点Q的距离相等?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数的图象与反比例函数的图象交于A(﹣3,1)、B(m,3)两点,
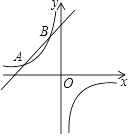
(1)求反比例函数和一次函数的解析式;
(2)写出使一次函数的值大于反比例函数的x的取值范围;
(3)连接AO、BO,求△ABO的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2)。
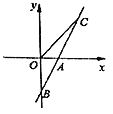
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△AOC =2,求点C的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标分别为A(1,1),B(2,﹣1),C(﹣2,﹣1),D(﹣1,1).以A为对称中心作点P(0,2)的对称点P1,以B为对称中心作点P1的对称点P2,以C为对称中心作点P2的对称点P3,以D为对称中心作点P3的对称点P4,…,重复操作依次得到点P1,P2,…,则点P2010的坐标是( )
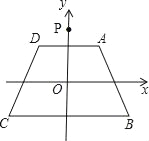
A. (2010,2) B. (2010,﹣2) C. (2012,﹣2) D. (0,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
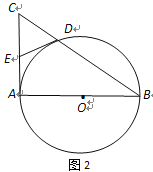
【题目】已知AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点D(如图1).
(1)若AB=2,∠B=30°,求CD的长;
(2) 取AC的中点E,连结D、E(如图2),求证:DE与⊙O相切.

【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】分析:![]() 连接AD ,根据AC是⊙O的切线,AB是⊙O的直径,得到∠CAB=∠ADB=90°,根据∠B=30°,解直角三角形求得
连接AD ,根据AC是⊙O的切线,AB是⊙O的直径,得到∠CAB=∠ADB=90°,根据∠B=30°,解直角三角形求得![]() 的长度.
的长度.
![]() 连接OD,AD.根据DE=CE=EA,∠EDA=∠EAD. 根据OD=OA,得到
连接OD,AD.根据DE=CE=EA,∠EDA=∠EAD. 根据OD=OA,得到
∠ODA=∠DAO,得到∠EDA+∠ODA=∠EAD+∠DAO.得到∠EDO=90°即可.
详解:(1)如图,连接AD ,
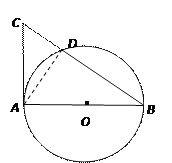
∵AC是⊙O的切线,AB是⊙O的直径,
∴∠CAB=∠ADB=90°,
∴ΔCAB,ΔCAD均是直角三角形.
∴∠CAD=∠B=30°.
在RtΔCAB中,AC=ABtan30°=![]()
∴在RtΔCAD中,CD=ACsin30°=![]()
(2)如图,连接OD,AD.

∵AC是⊙O的切线,AB是⊙O的直径,
∴∠CAB=∠ADB=∠ADC=90°,
又∵E为AC中点,
∴DE=CE=EA,
∴∠EDA=∠EAD.
∵OD=OA,
∴∠ODA=∠DAO,
∴∠EDA+∠ODA=∠EAD+∠DAO.
即:∠EDO=∠EAO=90°.
又点D在⊙O上,因此DE与⊙O相切.
点睛:考查解直角三角形,圆周角定理,切线的判定与性质等,属于圆的综合题,比较基础.注意切线的证明方法,是高频考点.
【题型】解答题
【结束】
21
【题目】课外活动时间,甲、乙、丙、丁4名同学相约进行羽毛球比赛.
(1)如果将4名同学随机分成两组进行对打,求恰好选中甲乙两人对打的概率;
(2)如果确定由丁担任裁判,用“手心、手背”的方法在另三人中竞选两人进行比赛.竞选规则是:三人同时伸出“手心”或“手背”中的一种手势,如果恰好只有两人伸出的手势相同,那么这两人上场,否则重新竞选.这三人伸出“手心”或“手背”都是随机的,求一次竞选就能确定甲、乙进行比赛的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com